publications
Publications in reversed chronological order by date of preprint.
All of my papers are available on the arXiv and on my Google Scholar page.
-
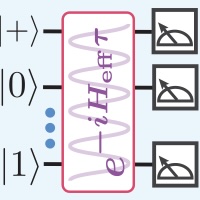 Ansatz-free Hamiltonian learning with Heisenberg-limited scalingHong-Ye Hu, Muzhou Ma, Weiyuan Gong, Qi Ye, Yu Tong, Steven T. Flammia, and Susanne F. YelinarXiv:2502.11900, 2025.
Ansatz-free Hamiltonian learning with Heisenberg-limited scalingHong-Ye Hu, Muzhou Ma, Weiyuan Gong, Qi Ye, Yu Tong, Steven T. Flammia, and Susanne F. YelinarXiv:2502.11900, 2025.Learning the unknown interactions that govern a quantum system is crucial for quantum information processing, device benchmarking, and quantum sensing. The problem, known as Hamiltonian learning, is well understood under the assumption that interactions are local, but this assumption may not hold for arbitrary Hamiltonians. Previous methods all require high-order inverse polynomial dependency with precision, unable to surpass the standard quantum limit and reach the gold standard Heisenberg-limited scaling. Whether Heisenberg-limited Hamiltonian learning is possible without prior assumptions about the interaction structures, a challenge we term \emphansatz-free Hamiltonian learning, remains an open question. In this work, we present a quantum algorithm to learn arbitrary sparse Hamiltonians without any structure constraints using only black-box queries of the system’s real-time evolution and minimal digital controls to attain Heisenberg-limited scaling in estimation error. Our method is also resilient to state-preparation-and-measurement errors, enhancing its practical feasibility. Moreover, we establish a fundamental trade-off between total evolution time and quantum control on learning arbitrary interactions, revealing the intrinsic interplay between controllability and total evolution time complexity for any learning algorithm. These results pave the way for further exploration into Heisenberg-limited Hamiltonian learning in complex quantum systems under minimal assumptions, potentially enabling new benchmarking and verification protocols.
@misc{2502.11900, archiveprefix = {arXiv}, author = {Hu, Hong-Ye and Ma, Muzhou and Gong, Weiyuan and Ye, Qi and Tong, Yu and Flammia, Steven T. and Yelin, Susanne F.}, doi = {10.48550/arXiv.2502.11900}, eprint = {2502.11900}, title = {{Ansatz-free Hamiltonian learning with Heisenberg-limited scaling}}, year = {2025} } -
 A Constructive Approach to Zauner’s Conjecture via the Stark ConjecturesMarcus Appleby, Steven T Flammia, and Gene S KopparXiv:2501.03970, 2025.
A Constructive Approach to Zauner’s Conjecture via the Stark ConjecturesMarcus Appleby, Steven T Flammia, and Gene S KopparXiv:2501.03970, 2025.We propose a construction of d^2 complex equiangular lines in \mathbbC^d, also known as SICPOVMs, which were conjectured by Zauner to exist for all d. The construction gives a putatively complete list of SICs with Weyl-Heisenberg symmetry in all dimensions d > 3. Specifically, we give an explicit expression for an object that we call a ghost SIC, which is constructed from the real multiplication values of a special function and which is Galois conjugate to a SIC. The special function, the Shintani-Faddeev modular cocycle, is a tuple of meromorphic functions indexed by a congruence subgroup of \mathrmSL_2(\mathbbZ). We prove that our construction gives a valid SIC in every case assuming two conjectures: the order-1 abelian Stark conjecture for real quadratic fields and a special value identity for the Shintani-Faddeev modular cocycle. The former allows us to prove that the ghost and the SIC are Galois conjugate over an extension of \mathbbQ(\sqrt∆) where ∆= (d+1)(d-3), while the latter allows us to prove idempotency of the presumptive fiducial projector. We provide computational tests of our SIC construction by cross-validating it with known exact solutions, with the numerical work of Scott and Grassl, and by constructing four numerical examples of inequivalent SICs in d = 100, three of which are new. We further consider rank-r generalizations called r-SICs given by equichordal configurations of r-dimensional complex subspaces. We give similar conditional constructions for r-SICs for all r, d such that r(d-r) divides (d^2-1). Finally, we study the structure of the field extensions conjecturally generated by the r-SICs. If K is any real quadratic field, then either every abelian Galois extension of K, or else every abelian extension for which 2 is unramified, is generated by our construction; the former holds for a positive density of field discriminants.
@misc{2501.03970, archiveprefix = {arXiv}, author = {Appleby, Marcus and Flammia, Steven T and Kopp, Gene S}, doi = {10.48550/arXiv.2501.03970}, eprint = {2501.03970}, title = {{A Constructive Approach to Zauner's Conjecture via the Stark Conjectures}}, year = {2025} } -
 Chasing shadows with Gottesman-Kitaev-Preskill codesJonathan Conrad, Jens Eisert, and Steven T. FlammiaarXiv:2411.00235, 2024.
Chasing shadows with Gottesman-Kitaev-Preskill codesJonathan Conrad, Jens Eisert, and Steven T. FlammiaarXiv:2411.00235, 2024.The infinitude of the continuous variable (CV) phase space is a serious obstacle in designing randomized tomography schemes with provable performance guarantees. A typical strategy to circumvent this issue is to impose a regularization, such as a photon-number cutoff, to enable the definition of ensembles of random unitaries on effective subspaces. In this work, we consider the task of performing shadow tomography of a logical subsystem defined via the Gottesman-Kitaev-Preskill (GKP) error correcting code. In particular, we construct a logical shadow tomography protocol via twirling of CV-POVMs by displacement operators and Gaussian unitaries. In the special case of heterodyne measurement, the shadow tomography protocol yields a probabilistic decomposition of any input state into Gaussian states that simulate the encoded logical information of the input relative to a fixed GKP code and we prove bounds on the Gaussian compressibility of states in this setting. For photon-parity measurements, logical GKP shadow tomography is equivalent to a Wigner sampling protocol for which we develop the appropriate sampling schemes and finally, using the existence of a Haar measure over symplectic lattices, we derive a Wigner sampling scheme via random GKP codes. This protocol establishes, via explicit sample complexity bounds, how Wigner samples of any input state from random points relative to a random GKP codes can be used to estimate any sufficiently bounded observable on CV space.
@misc{2411.00235, archiveprefix = {arXiv}, author = {Conrad, Jonathan and Eisert, Jens and Flammia, Steven T.}, doi = {10.48550/arXiv.2411.00235}, eprint = {2411.00235}, title = {{Chasing shadows with Gottesman-Kitaev-Preskill codes}}, year = {2024} } -
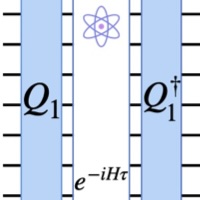 Learning k-body Hamiltonians via compressed sensingMuzhou Ma, Steven T. Flammia, John Preskill, and Yu TongarXiv:2410.18928, 2024.
Learning k-body Hamiltonians via compressed sensingMuzhou Ma, Steven T. Flammia, John Preskill, and Yu TongarXiv:2410.18928, 2024.We study the problem of learning a k-body Hamiltonian with M unknown Pauli terms that are not necessarily geometrically local. We propose a protocol that learns the Hamiltonian to precision εwith total evolution time O(M1/2+1/p/ε) up to logarithmic factors, where the error is quantified by the ℓp-distance between Pauli coefficients. Our learning protocol uses only single-qubit control operations and a GHZ state initial state, is non-adaptive, is robust against SPAM errors, and performs well even if M and k are not precisely known in advance or if the Hamiltonian is not exactly M-sparse. Methods from the classical theory of compressed sensing are used for efficiently identifying the M terms in the Hamiltonian from among all possible k-body Pauli operators. We also provide a lower bound on the total evolution time needed in this learning task, and we discuss the operational interpretations of the ℓ1 and ℓ2 error metrics. In contrast to previous works, our learning protocol requires neither geometric locality nor any other relaxed locality conditions.
@misc{2410.18928, archiveprefix = {arXiv}, author = {Ma, Muzhou and Flammia, Steven T. and Preskill, John and Tong, Yu}, doi = {10.48550/arXiv.2410.18928}, eprint = {2410.18928}, title = {{Learning $k$-body Hamiltonians via compressed sensing}}, year = {2024} } -
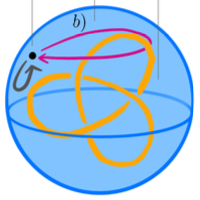 Fiber Bundle Fault Tolerance of GKP CodesAnsgar G. Burchards, Steven T. Flammia, and Jonathan ConradarXiv:2410.07332, 2024.
Fiber Bundle Fault Tolerance of GKP CodesAnsgar G. Burchards, Steven T. Flammia, and Jonathan ConradarXiv:2410.07332, 2024.We investigate multi-mode GKP (Gottesman–Kitaev–Preskill) quantum error-correcting codes from a geometric perspective. First, we construct their moduli space as a quotient of groups and exhibit it as a fiber bundle over the moduli space of symplectically integral lattices. We then establish the Gottesman–Zhang conjecture for logical GKP Clifford operations, showing that all such gates arise from parallel transport with respect to a flat connection on this space. Specifically, non-trivial Clifford operations correspond to topologically non-contractible paths on the space of GKP codes, while logical identity operations correspond to contractible paths.
@misc{2410.07332, archiveprefix = {arXiv}, author = {Burchards, Ansgar G. and Flammia, Steven T. and Conrad, Jonathan}, doi = {10.48550/arXiv.2410.07332}, eprint = {2410.07332}, title = {{Fiber Bundle Fault Tolerance of GKP Codes}}, year = {2024} } -
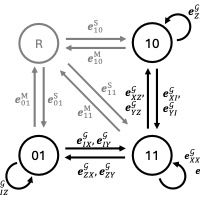 Efficient self-consistent learning of gate set Pauli noiseSenrui Chen, Zhihan Zhang, Liang Jiang, and Steven T. FlammiaarXiv:2410.03906, 2024.
Efficient self-consistent learning of gate set Pauli noiseSenrui Chen, Zhihan Zhang, Liang Jiang, and Steven T. FlammiaarXiv:2410.03906, 2024.Understanding quantum noise is an essential step towards building practical quantum information processing systems. Pauli noise is a useful model that has been widely applied in quantum benchmarking, error mitigation, and error correction. Despite intensive study, most existing works focus on learning Pauli noise channels associated with some specific gates rather than treating the gate set as a whole. A learning algorithm that is self-consistent, complete, and efficient at the same time is yet to be established. In this work, we study the task of gate set Pauli noise learning, where a set of quantum gates, state preparation, and measurements all suffer from unknown Pauli noise channels with a customized noise ansatz. Using tools from algebraic graph theory, we analytically characterize the self-consistently learnable degrees of freedom for Pauli noise models with arbitrary linear ansatz, and design experiments to efficiently learn all the learnable information. Specifically, we show that all learnable information about the gate noise can be learned to relative precision, under mild assumptions on the noise ansatz. We then demonstrate the flexibility of our theory by applying it to concrete physically motivated ansatzs (such as spatially local or quasi-local noise) and experimentally relevant gate sets (such as parallel CZ gates). These results not only enhance the theoretical understanding of quantum noise learning, but also provide a feasible recipe for characterizing existing and near-future quantum information processing devices.
@misc{2410.03906, archiveprefix = {arXiv}, author = {Chen, Senrui and Zhang, Zhihan and Jiang, Liang and Flammia, Steven T.}, doi = {10.48550/arXiv.2410.03906}, eprint = {2410.03906}, title = {Efficient self-consistent learning of gate set Pauli noise}, year = {2024} } -
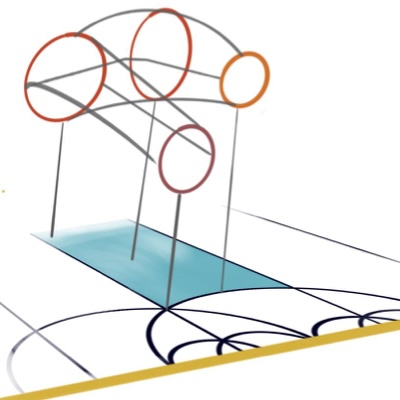 Lattices, Gates, and Curves: GKP codes as a Rosetta stoneJonathan Conrad, Ansgar G. Burchards, and Steven T. FlammiaarXiv:2407.03270, 2024.
Lattices, Gates, and Curves: GKP codes as a Rosetta stoneJonathan Conrad, Ansgar G. Burchards, and Steven T. FlammiaarXiv:2407.03270, 2024.Gottesman–Kitaev–Preskill (GKP) codes are a promising candidate for implementing fault tolerant quantum computation in quantum harmonic oscillator systems such as superconducting resonators, optical photons and trapped ions, and in recent years theoretical and experimental evidence for their utility has steadily grown. It is known that logical Clifford operations on GKP codes can be implemented fault tolerantly using only Gaussian operations, and several theoretical investigations have illuminated their general structure. In this work, we explain how GKP Clifford gates arise as symplectic automorphisms of the corresponding GKP lattice and show how they are identified with the mapping class group of suitable genus n surfaces. This correspondence introduces a topological interpretation of fault tolerance for GKP codes and motivates the connection between GKP codes (lattices), their Clifford gates, and algebraic curves, which we explore in depth. For a single-mode GKP code, we identify the space of all GKP codes with the moduli space of elliptic curves, given by the three sphere with a trefoil knot removed, and explain how logical degrees of freedom arise from the choice of a level structure on the corresponding curves. We discuss how the implementation of Clifford gates corresponds to homotopically nontrivial loops on the space of all GKP codes and show that the modular Rademacher function describes a topological invariant for certain Clifford gates implemented by such loops. Finally, we construct a universal family of GKP codes and show how it gives rise to an explicit construction of fiber bundle fault tolerance as proposed by Gottesman and Zhang for the GKP code. On our path towards understanding this correspondence, we introduce a general algebraic geometric perspective on GKP codes and their moduli spaces, which uncovers a map towards many possible routes of future research.
@misc{2407.03270, archiveprefix = {arXiv}, author = {Conrad, Jonathan and Burchards, Ansgar G. and Flammia, Steven T.}, doi = {10.48550/arXiv.2407.03270}, eprint = {2407.03270}, title = {{Lattices, Gates, and Curves: GKP codes as a Rosetta stone}}, year = {2024} } -
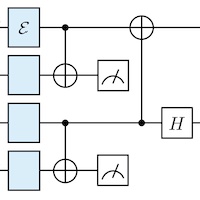 Fault-Tolerant Quantum Memory using Low-Depth Random Circuit CodesJon Nelson, Gregory Bentsen, Steven T. Flammia, and Michael J. GullansarXiv:2311.17985, 2023.
Fault-Tolerant Quantum Memory using Low-Depth Random Circuit CodesJon Nelson, Gregory Bentsen, Steven T. Flammia, and Michael J. GullansarXiv:2311.17985, 2023.Low-depth random circuit codes possess many desirable properties for quantum error correction but have so far only been analyzed in the code capacity setting where it is assumed that encoding gates and syndrome measurements are noiseless. In this work, we design a fault-tolerant distillation protocol for preparing encoded states of one-dimensional random circuit codes even when all gates and measurements are subject to noise. This is sufficient for fault-tolerant quantum memory since these encoded states can then be used as ancillas for Steane error correction. We show through numerical simulations that our protocol can correct erasure errors up to an error rate of 2%. In addition, we also extend results in the code capacity setting by developing a maximum likelihood decoder for depolarizing noise similar to work by Darmawan et al. As in their work, we formulate the decoding problem as a tensor network contraction and show how to contract the network efficiently by exploiting the low-depth structure. Replacing the tensor network with a so-called “tropical” tensor network, we also show how to perform minimum weight decoding. With these decoders, we are able to numerically estimate the depolarizing error threshold of finite-rate random circuit codes and show that this threshold closely matches the hashing bound even when the decoding is sub-optimal.
@misc{2311.17985, author = {Nelson, Jon and Bentsen, Gregory and Flammia, Steven T. and Gullans, Michael J.}, archiveprefix = {arXiv}, doi = {10.48550/arXiv.2311.17985}, eprint = {2311.17985}, title = {{Fault-Tolerant Quantum Memory using Low-Depth Random Circuit Codes}}, year = {2023} } -
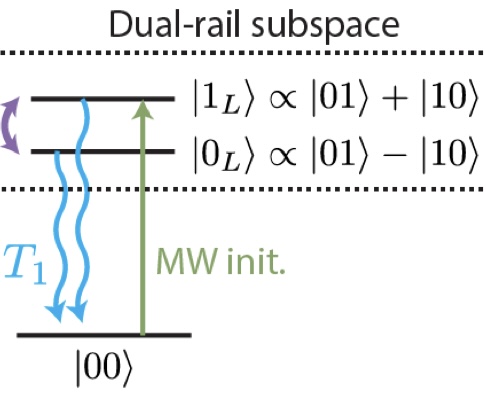 Demonstrating a Long-Coherence Dual-Rail Erasure Qubit Using Tunable TransmonsH. Levine, A. Haim, J. S. C. Hung, N. Alidoust, M. Kalaee, L. DeLorenzo, E. A. Wollack, P. Arrangoiz-Arriola, A. Khalajhedayati, R. Sanil, and 103 more authorsPhysical Review X, 14 011051 2024.
Demonstrating a Long-Coherence Dual-Rail Erasure Qubit Using Tunable TransmonsH. Levine, A. Haim, J. S. C. Hung, N. Alidoust, M. Kalaee, L. DeLorenzo, E. A. Wollack, P. Arrangoiz-Arriola, A. Khalajhedayati, R. Sanil, and 103 more authorsPhysical Review X, 14 011051 2024.Quantum error correction with erasure qubits promises significant advantages over standard error correction due to favorable thresholds for erasure errors. To realize this advantage in practice requires a qubit for which nearly all errors are such erasure errors, and the ability to check for erasure errors without dephasing the qubit. We demonstrate that a "dual-rail qubit" consisting of a pair of resonantly coupled transmons can form a highly coherent erasure qubit, where transmon T1 errors are converted into erasure errors and residual dephasing is strongly suppressed, leading to millisecond-scale coherence within the qubit subspace. We show that single-qubit gates are limited primarily by erasure errors, with erasure probability perasure=2.19(2)×10−3 per gate while the residual errors are ∼40 times lower. We further demonstrate mid-circuit detection of erasure errors while introducing < 0.1% dephasing error per check. Finally, we show that the suppression of transmon noise allows this dual-rail qubit to preserve high coherence over a broad tunable operating range, offering an improved capacity to avoid frequency collisions. This work establishes transmon-based dual-rail qubits as an attractive building block for hardware-efficient quantum error correction.
@article{2307.08737, author = {Levine, H. and Haim, A. and Hung, J. S. C. and Alidoust, N. and Kalaee, M. and DeLorenzo, L. and Wollack, E. A. and Arrangoiz-Arriola, P. and Khalajhedayati, A. and Sanil, R. and Moradinejad, H. and Vaknin, Y. and Kubica, A. and Hover, D. and Aghaeimeibodi, S. and Alcid, J. A. and Baek, C. and Barnett, J. and Bawdekar, K. and Bienias, P. and Carson, H. A. and Chen, C. and Chen, L. and Chinkezian, H. and Chisholm, E. M. and Clifford, A. and Cosmic, R. and Crisosto, N. and Dalzell, A. M. and Davis, E. and D’Ewart, J. M. and Diez, S. and D’Souza, N. and Dumitrescu, P. T. and Elkhouly, E. and Fang, M. T. and Fang, Y. and Flammia, S. and Fling, M. J. and Garcia, G. and Gharzai, M. K. and Gorshkov, A. V. and Gray, M. J. and Grimberg, S. and Grimsmo, A. L. and Hann, C. T. and He, Y. and Heidel, S. and Howell, S. and Hunt, M. and Iverson, J. and Jarrige, I. and Jiang, L. and Jones, W. M. and Karabalin, R. and Karalekas, P. J. and Keller, A. J. and Lasi, D. and Lee, M. and Ly, V. and MacCabe, G. and Mahuli, N. and Marcaud, G. and Matheny, M. H. and McArdle, S. and McCabe, G. and Merton, G. and Miles, C. and Milsted, A. and Mishra, A. and Moncelsi, L. and Naghiloo, M. and Noh, K. and Oblepias, E. and Ortuno, G. and Owens, J. C. and Pagdilao, J. and Panduro, A. and Paquette, J.-P. and Patel, R. N. and Peairs, G. and Perello, D. J. and Peterson, E. C. and Ponte, S. and Putterman, H. and Refael, G. and Reinhold, P. and Resnick, R. and Reyna, O. A. and Rodriguez, R. and Rose, J. and Rubin, A. H. and Runyan, M. and Ryan, C. A. and Sahmoud, A. and Scaffidi, T. and Shah, B. and Siavoshi, S. and Sivarajah, P. and Skogland, T. and Su, C.-J. and Swenson, L. J. and Sylvia, J. and Teo, S. M. and Tomada, A. and Torlai, G. and Wistrom, M. and Zhang, K. and Zuk, I. and Clerk, A. A. and Brandão, F. G. S. L. and Retzker, A. and Painter, O.}, archiveprefix = {arXiv}, doi = {10.1103/physrevx.14.011051}, eprint = {2307.08737}, title = {Demonstrating a Long-Coherence Dual-Rail Erasure Qubit Using Tunable Transmons}, journal = {Physical Review X}, volume = {14}, pages = {011051}, year = {2024} } -
 Quantum chi-squared tomography and mutual information testingSteven T. Flammia, and Ryan O’DonnellQuantum, 8 1381 2024.
Quantum chi-squared tomography and mutual information testingSteven T. Flammia, and Ryan O’DonnellQuantum, 8 1381 2024.For quantum state tomography on rank-r dimension-d states, we show that Õ(r.5 d1.5/ε) ≤ Õ(d2/ε) copies suffice for accuracy ε with respect to (Bures) 𝛘2-divergence, and Õ(rd/ε) copies suffice for accuracy ε with respect to quantum relative entropy. The best previous bound was Õ(rd/ε) ≤ Õ(d2/ε) with respect to infidelity; our results are an improvement since infidelity is bounded above by both the relative entropy and the 𝛘2-divergence.
For algorithms that are required to use single-copy measurements, we show that Õ(r1.5 d1.5/ε) ≤ Õ(d3/ε) copies suffice for 𝛘2-divergence, and Õ(r2 d/ε) suffice for relative entropy.
Using this tomography algorithm, we show that Õ(d2.5/ε) copies of a d×d-dimensional bipartite state suffice to test if it has quantum mutual information 0 or at least ε. As a corollary, we also improve the best known sample complexity for the classical version of mutual information testing to Õ(d/ε).
@article{2305.18519, author = {Flammia, Steven T. and O'Donnell, Ryan}, archiveprefix = {arXiv}, doi = {10.22331/q-2024-06-20-1381}, journal = {Quantum}, volume = {8}, pages = {1381}, eprint = {2305.18519}, title = {Quantum chi-squared tomography and mutual information testing}, year = {2024} } -
 Learning correlated noise in a 39-qubit quantum processorRobin Harper, and Steven T. FlammiaPRX Quantum, 4 040311 2023.
Learning correlated noise in a 39-qubit quantum processorRobin Harper, and Steven T. FlammiaPRX Quantum, 4 040311 2023.Building error-corrected quantum computers relies crucially on measuring and modeling noise on candidate devices. In particular, optimal error correction requires knowing the noise that occurs in the device as it executes the circuits required for error correction. As devices increase in size we will become more reliant on efficient models of this noise. However, such models must still retain the information required to optimize the algorithms used for error correction. Here we propose a method of extracting detailed information of the noise in a device running syndrome extraction circuits. We introduce and execute an experiment on a superconducting device using 39 of its qubits in a surface code doing repeated rounds of syndrome extraction, but omitting the mid-circuit measurement and reset. We show how to extract from the 20 data qubits the information needed to build noise models of various sophistication in the form of graphical models. These models give efficient descriptions of noise in large-scale devices and are designed to illuminate the effectiveness of error correction against correlated noise. Our estimates are furthermore precise: we learn a consistent global distribution where all one- and two-qubit error rates are known to a relative error of 0.1%. By extrapolating our experimentally learned noise models towards lower error rates, we demonstrate that accurate correlated noise models are increasingly important for successfully predicting sub-threshold behavior in quantum error correction experiments.
@article{2303.00780, author = {Harper, Robin and Flammia, Steven T.}, archiveprefix = {arXiv}, doi = {10.1103/PRXQuantum.4.040311}, eprint = {2303.00780}, journal = {PRX Quantum}, pages = {040311}, title = {Learning correlated noise in a 39-qubit quantum processor}, volume = {4}, year = {2023} } -
 Foundations for learning from noisy quantum experimentsHsin-Yuan Huang, Steven T. Flammia, and John PreskillarXiv:2204.13691, 2022.
Foundations for learning from noisy quantum experimentsHsin-Yuan Huang, Steven T. Flammia, and John PreskillarXiv:2204.13691, 2022.Understanding what can be learned from experiments is central to scientific progress. In this work, we use a learning-theoretic perspective to study the task of learning physical operations in a quantum machine when all operations (state preparation, dynamics, and measurement) are a priori unknown. We prove that, without any prior knowledge, if one can explore the full quantum state space by composing the operations, then every operation can be learned. When one cannot explore the full state space but all operations are approximately known and noise in Clifford gates is gate-independent, we find an efficient algorithm for learning all operations up to a single unlearnable parameter characterizing the fidelity of the initial state. For learning a noise channel on Clifford gates to a fixed accuracy, our algorithm uses quadratically fewer experiments than previously known protocols. Under more general conditions, the true description of the noise can be unlearnable; for example, we prove that no benchmarking protocol can learn gate-dependent Pauli noise on Clifford+T gates even under perfect state preparation and measurement. Despite not being able to learn the noise, we show that a noisy quantum computer that performs entangled measurements on multiple copies of an unknown state can yield a large advantage in learning properties of the state compared to a noiseless device that measures individual copies and then processes the measurement data using a classical computer. Concretely, we prove that noisy quantum computers with two-qubit gate error rate ϵ can achieve a learning task using N copies of the state, while NΩ(1/ϵ) copies are required classically.
@misc{2204.13691, author = {Huang, Hsin-Yuan and Flammia, Steven T. and Preskill, John}, archiveprefix = {arXiv}, doi = {10.48550/arXiv.2204.13691}, eprint = {2204.13691}, title = {Foundations for learning from noisy quantum experiments}, year = {2022} } -
 The randomized measurement toolboxAndreas Elben, Steven T. Flammia, Hsin-Yuan Huang, Richard Kueng, John Preskill, Benoı̂t Vermersch, and Peter ZollerNature Review Physics, 5 9–24 2022.
The randomized measurement toolboxAndreas Elben, Steven T. Flammia, Hsin-Yuan Huang, Richard Kueng, John Preskill, Benoı̂t Vermersch, and Peter ZollerNature Review Physics, 5 9–24 2022.Increasingly sophisticated programmable quantum simulators and quantum computers are opening unprecedented opportunities for exploring and exploiting the properties of highly entangled complex quantum systems. The complexity of large quantum systems is the source of their power, but also makes them difficult to control precisely or characterize accurately using measured classical data. We review recently developed protocols for probing the properties of complex many-qubit systems using measurement schemes that are practical using today’s quantum platforms. In all these protocols, a quantum state is repeatedly prepared and measured in a randomly chosen basis; then a classical computer processes the measurement outcomes to estimate the desired property. The randomization of the measurement procedure has distinct advantages; for example, a single data set can be employed multiple times to pursue a variety of applications, and imperfections in the measurements are mapped to a simplified noise model that can more easily be mitigated. We discuss a range of use cases that have already been realized in quantum devices, including Hamiltonian simulation tasks, probes of quantum chaos, measurements of nonlocal order parameters, and comparison of quantum states produced in distantly separated laboratories. By providing a workable method for translating a complex quantum state into a succinct classical representation that preserves a rich variety of relevant physical properties, the randomized measurement toolbox strengthens our ability to grasp and control the quantum world.
@article{2203.11374, author = {Elben, Andreas and Flammia, Steven T. and Huang, Hsin-Yuan and Kueng, Richard and Preskill, John and Vermersch, Beno{\^\i}t and Zoller, Peter}, archiveprefix = {arXiv}, doi = {10.1038/s42254-022-00535-2}, eprint = {2203.11374}, journal = {Nature Review Physics}, number = {1}, pages = {9--24}, title = {The randomized measurement toolbox}, volume = {5}, year = {2022} } -
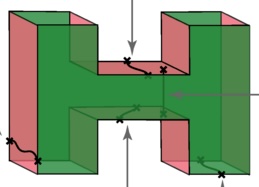 Improved decoding of circuit noise and fragile boundaries of tailored surface codesOscar Higgott, Thomas C Bohdanowicz, Aleksander Kubica, Steven T Flammia, and Earl T CampbellPhysical Review X, 13 031007 2023.
Improved decoding of circuit noise and fragile boundaries of tailored surface codesOscar Higgott, Thomas C Bohdanowicz, Aleksander Kubica, Steven T Flammia, and Earl T CampbellPhysical Review X, 13 031007 2023.Realizing the full potential of quantum computation requires quantum error correction (QEC), with most recent breakthrough demonstrations of QEC using the surface code. QEC codes use multiple noisy physical qubits to encode information in fewer logical qubits, enabling the identification of errors through a decoding process. This process increases the logical fidelity (or accuracy) making the computation more reliable. However, most fast (efficient runtime) decoders neglect important noise characteristics, thereby reducing their accuracy. In this work, we introduce decoders that are both fast and accurate, and can be used with a wide class of QEC codes including the surface code. Our decoders, named belief-matching and belief-find, exploit all noise information and thereby unlock higher accuracy demonstrations of QEC. Using the surface code threshold as a performance metric, we observe a threshold at 0.94% error probability for our decoders, outperforming the 0.82% threshold for a standard minimum-weight perfect matching decoder. We also tested our belief-matching decoders in a theoretical case study of codes tailored to a biased noise model. We find that the decoders led to a much higher threshold and lower qubit overhead in the tailored surface code with respect to the standard, square surface code. Surprisingly, in the well-below threshold regime, the rectangular surface code becomes more resource-efficient than the tailored surface code, due to a previously unnoticed phenomenon that we call "fragile boundaries". Our decoders outperform all other fast decoders in terms of threshold and accuracy, enabling better results in current quantum error correction experiments and opening up new areas for theoretical case studies.
@article{2203.04948, author = {Higgott, Oscar and Bohdanowicz, Thomas C and Kubica, Aleksander and Flammia, Steven T and Campbell, Earl T}, archiveprefix = {arXiv}, journal = {Physical Review X}, volume = {13}, issue = {3}, pages = {031007}, eprint = {2203.04948}, doi = {10.1103/PhysRevX.13.031007}, title = {Improved decoding of circuit noise and fragile boundaries of tailored surface codes}, year = {2023} } -
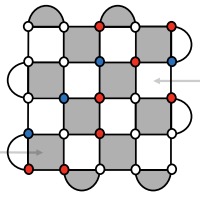 Clifford-deformed Surface CodesArpit Dua, Aleksander Kubica, Liang Jiang, Steven T. Flammia, and Michael J. GullansPRX Quantum, 5 010347 2024.
Clifford-deformed Surface CodesArpit Dua, Aleksander Kubica, Liang Jiang, Steven T. Flammia, and Michael J. GullansPRX Quantum, 5 010347 2024.Various realizations of Kitaev’s surface code perform surprisingly well for biased Pauli noise. Attracted by these potential gains, we study the performance of Clifford-deformed surface codes (CDSCs) obtained from the surface code by the application of single-qubit Clifford operators. We first analyze CDSCs on the 3×3 square lattice and find that depending on the noise bias, their logical error rates can differ by orders of magnitude. To explain the observed behavior, we introduce the effective distance d’, which reduces to the standard distance for unbiased noise. To study CDSC performance in the thermodynamic limit, we focus on random CDSCs. Using the statistical mechanical mapping for quantum codes, we uncover a phase diagram that describes random CDSCs with 50% threshold at infinite bias. In the high-threshold region, we further demonstrate that typical code realizations at finite bias outperform the thresholds and subthreshold logical error rates of the best known translationally invariant codes.
@article{2201.07802, author = {Dua, Arpit and Kubica, Aleksander and Jiang, Liang and Flammia, Steven T. and Gullans, Michael J.}, archiveprefix = {arXiv}, journal = {PRX Quantum}, volume = {5}, issue = {1}, pages = {010347}, eprint = {2201.07802}, doi = {10.1103/PRXQuantum.5.010347}, title = {Clifford-deformed Surface Codes}, year = {2024} } -
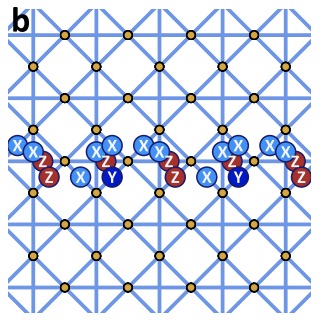 Free-Fermion Subsystem CodesAdrian Chapman, Steven T. Flammia, and Alicia J. KollárPRX Quantum, 3 030321 2022.
Free-Fermion Subsystem CodesAdrian Chapman, Steven T. Flammia, and Alicia J. KollárPRX Quantum, 3 030321 2022.We consider quantum error-correcting subsystem codes whose gauge generators realize a translation-invariant, free-fermion-solvable spin model. In this setting, errors are suppressed by a Hamiltonian whose terms are the gauge generators of the code and whose exact spectrum and eigenstates can be found via a generalized Jordan-Wigner transformation. Such solutions are characterized by the frustration graph of the Hamiltonian: the graph whose vertices are Hamiltonian terms, which are neighboring if the terms anticommute. We provide methods for embedding a given frustration graph in the anticommutation relations of a spin model and present the first known example of an exactly solvable spin model with a two-dimensional free-fermion description and exact topological qubits. This model can be viewed as a free-fermionized version of the two-dimensional Bacon-Shor code. Using graph-theoretic tools to study the unit cell, we give an efficient algorithm for deciding if a given translation-invariant spin model is solvable, and explicitly construct the solution. Further, we examine the energetics of these exactly solvable models from the graph-theoretic perspective and show that the relevant gaps of the spin model correspond to known graph-theoretic quantities: the skew energy and the median eigenvalue of an oriented graph. Finally, we numerically search for models which have large spectral gaps above the ground state spin configuration and thus exhibit particularly robust thermal suppression of errors. These results suggest that optimal models will have low dimensionality and odd coordination numbers, and that the primary limit to energetic error suppression is the skew energy difference between different symmetry sectors rather than single-particle excitations of the free fermions.
@article{2201.07254, author = {Chapman, Adrian and Flammia, Steven T. and Koll{\'a}r, Alicia J.}, archiveprefix = {arXiv}, doi = {10.1103/PRXQuantum.3.030321}, eprint = {2201.07254}, journal = {PRX Quantum}, pages = {030321}, title = {Free-Fermion Subsystem Codes}, volume = {3}, year = {2022} } -
 Averaged circuit eigenvalue samplingSteven T. FlammiaIn 17th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2022), 232 4:1–4:10 2022.
Averaged circuit eigenvalue samplingSteven T. FlammiaIn 17th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2022), 232 4:1–4:10 2022.We introduce ACES, a method for scalable noise metrology of quantum circuits that stands for Averaged Circuit Eigenvalue Sampling. It simultaneously estimates the individual error rates of all the gates in collections of quantum circuits, and can even account for space and time correlations between these gates. ACES strictly generalizes randomized benchmarking (RB), interleaved RB, simultaneous RB, and several other related techniques. However, ACES provides much more information and provably works under strictly weaker assumptions than these techniques. Finally, ACES is extremely scalable: we demonstrate with numerical simulations that it simultaneously and precisely estimates all the Pauli error rates on every gate and measurement in a 100 qubit quantum device using fewer than 20 relatively shallow Clifford circuits and an experimentally feasible number of samples. By learning the detailed gate errors for large quantum devices, ACES opens new possibilities for error mitigation, bespoke quantum error correcting codes and decoders, customized compilers, and more.
@inproceedings{2108.05803, author = {Flammia, Steven T.}, archiveprefix = {arXiv}, doi = {10.4230/LIPIcs.TQC.2022.4}, eprint = {2108.05803}, title = {Averaged circuit eigenvalue sampling}, booktitle = {17th Conference on the Theory of Quantum Computation, Communication and Cryptography (TQC 2022)}, pages = {4:1--4:10}, series = {Leibniz International Proceedings in Informatics (LIPIcs)}, year = {2022}, volume = {232}, editor = {Le Gall, Fran\c{c}ois and Morimae, Tomoyuki}, publisher = {Schloss Dagstuhl -- Leibniz-Zentrum f{\"u}r Informatik}, address = {Dagstuhl, Germany} } -
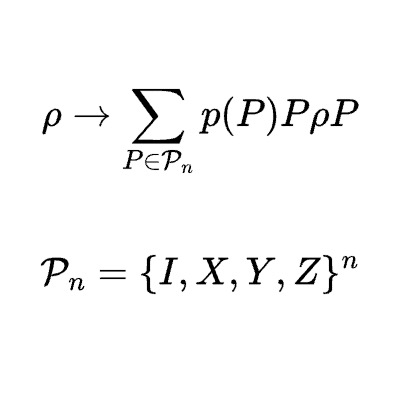 Pauli error estimation via Population RecoverySteven T. Flammia, and Ryan O’DonnellQuantum, 5 549 2021.
Pauli error estimation via Population RecoverySteven T. Flammia, and Ryan O’DonnellQuantum, 5 549 2021.Motivated by estimation of quantum noise models, we study the problem of learning a Pauli channel, or more generally the Pauli error rates of an arbitrary channel. By employing a novel reduction to the “Population Recovery” problem, we give an extremely simple algorithm that learns the Pauli error rates of an n-qubit channel to precision ϵ in ℓ∞ using just O(1/ϵ2) \log(n/ϵ) applications of the channel. This is optimal up to the logarithmic factors. Our algorithm uses only unentangled state preparation and measurements, and the post-measurement classical runtime is just an O(1/ϵ) factor larger than the measurement data size. It is also impervious to a limited model of measurement noise where heralded measurement failures occur independently with probability ≤1/4. We then consider the case where the noise channel is close to the identity, meaning that the no-error outcome occurs with probability 1−η. In the regime of small η we extend our algorithm to achieve multiplicative precision 1±ϵ (i.e., additive precision ϵη) using just O(1/ϵ2 η) \log(n/ϵ) applications of the channel.
@article{2105.02885, author = {Flammia, Steven T. and O'Donnell, Ryan}, doi = {10.22331/q-2021-09-23-549}, archiveprefix = {arXiv}, eprint = {2105.02885}, journal = {Quantum}, pages = {549}, title = {Pauli error estimation via Population Recovery}, volume = {5}, year = {2021} } -
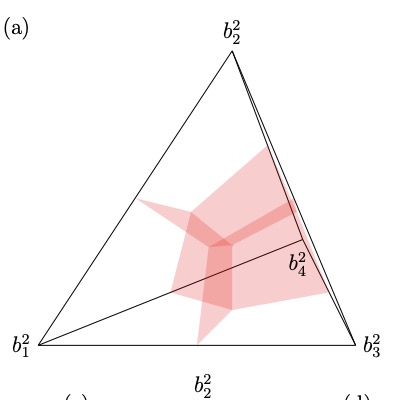 Free fermions behind the disguiseSamuel J. Elman, Adrian Chapman, and Steven T. FlammiaComm. Math. Phys., 388 969–1003 2021.
Free fermions behind the disguiseSamuel J. Elman, Adrian Chapman, and Steven T. FlammiaComm. Math. Phys., 388 969–1003 2021.An invaluable method for probing the physics of a quantum many-body spin system is a mapping to noninteracting effective fermions. We find such mappings using only the frustration graph G of a Hamiltonian H, i.e., the network of anticommutation relations between the Pauli terms in H in a given basis. Specifically, when G is (even-hole, claw)-free, we construct an explicit free-fermion solution for H using only this structure of G, even when no Jordan-Wigner transformation exists. The solution method is generic in that it applies for any values of the couplings. This mapping generalizes both the classic Lieb-Schultz-Mattis solution of the XY model and an exact solution of a spin chain recently given by Fendley, dubbed "free fermions in disguise." Like Fendley’s original example, the free-fermion operators that solve the model are generally highly nonlinear and nonlocal, but can nonetheless be found explicitly using a transfer operator defined in terms of the independent sets of G. The associated single-particle energies are calculated using the roots of the independence polynomial of G, which are guaranteed to be real by a result of Chudnovsky and Seymour. Furthermore, recognizing (even-hole, claw)-free graphs can be done in polynomial time, so recognizing when a spin model is solvable in this way is efficient. We give several example families of solvable models for which no Jordan-Wigner solution exists, and we give a detailed analysis of such a spin chain having 4-body couplings using this method.
@article{2012.07857, author = {Elman, Samuel J. and Chapman, Adrian and Flammia, Steven T.}, doi = {10.1007/s00220-021-04220-w}, archiveprefix = {arXiv}, eprint = {2012.07857}, journal = {Comm. Math. Phys.}, pages = {969--1003}, title = {Free fermions behind the disguise}, volume = {388}, year = {2021} } -
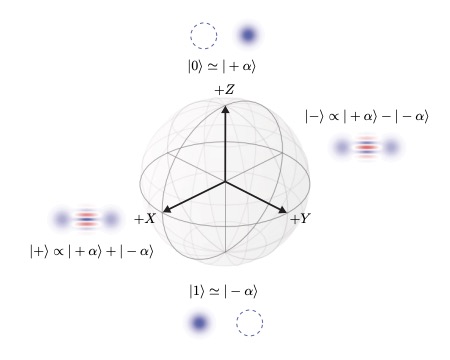 Building a fault-tolerant quantum computer using concatenated cat codesChristopher Chamberland, Kyungjoo Noh, Patricio Arrangoiz-Arriola, Earl T. Campbell, Connor T. Hann, Joseph Iverson, Harald Putterman, Thomas C. Bohdanowicz, Steven T. Flammia, Andrew Keller, and 6 more authorsPRX Quantum, 3 010329 2020.
Building a fault-tolerant quantum computer using concatenated cat codesChristopher Chamberland, Kyungjoo Noh, Patricio Arrangoiz-Arriola, Earl T. Campbell, Connor T. Hann, Joseph Iverson, Harald Putterman, Thomas C. Bohdanowicz, Steven T. Flammia, Andrew Keller, and 6 more authorsPRX Quantum, 3 010329 2020.We present a comprehensive architectural analysis for a proposed fault-tolerant quantum computer based on cat codes concatenated with outer quantum error-correcting codes. For the physical hardware, we propose a system of acoustic resonators coupled to superconducting circuits with a two-dimensional layout. Using estimated physical parameters for the hardware, we perform a detailed error analysis of measurements and gates, including CNOT and Toffoli gates. Having built a realistic noise model, we numerically simulate quantum error correction when the outer code is either a repetition code or a thin rectangular surface code. Our next step toward universal fault-tolerant quantum computation is a protocol for fault-tolerant Toffoli magic state preparation that significantly improves upon the fidelity of physical Toffoli gates at very low qubit cost. To achieve even lower overheads, we devise a new magic-state distillation protocol for Toffoli states. Combining these results together, we obtain realistic full-resource estimates of the physical error rates and overheads needed to run useful fault-tolerant quantum algorithms. We find that with around 1,000 superconducting circuit components, one could construct a fault-tolerant quantum computer that can run circuits which are currently intractable for classical computers. Hardware with 18,000 superconducting circuit components, in turn, could simulate the Hubbard model in a regime beyond the reach of classical computing.
@article{2012.04108, author = {Chamberland, Christopher and Noh, Kyungjoo and Arrangoiz-Arriola, Patricio and Campbell, Earl T. and Hann, Connor T. and Iverson, Joseph and Putterman, Harald and Bohdanowicz, Thomas C. and Flammia, Steven T. and Keller, Andrew and Refael, Gil and Preskill, John and Jiang, Liang and Safavi-Naeini, Amir H. and Painter, Oskar and Brand{\~a}o, Fernando G. S. L.}, doi = {10.1103/PRXQuantum.3.010329}, archiveprefix = {arXiv}, eprint = {2012.04108}, journal = {PRX Quantum}, pages = {010329}, title = {Building a fault-tolerant quantum computer using concatenated cat codes}, volume = {3}, year = {2020} } -
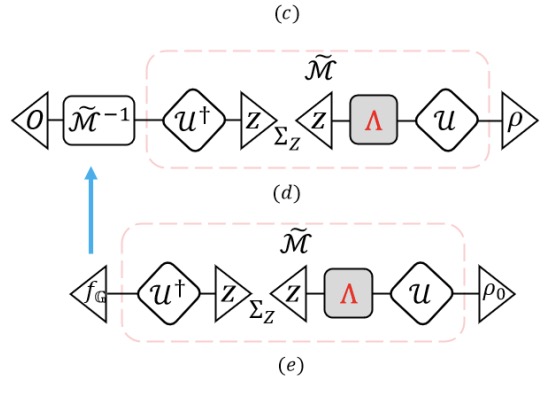 Robust shadow estimationSenrui Chen, Wenjun Yu, Pei Zeng, and Steven T. FlammiaPRX Quantum, 2 030348 2020.
Robust shadow estimationSenrui Chen, Wenjun Yu, Pei Zeng, and Steven T. FlammiaPRX Quantum, 2 030348 2020.Efficiently estimating properties of large and strongly coupled quantum systems is a central focus in many-body physics and quantum information theory. While quantum computers promise speedups for many such tasks, near-term devices are prone to noise that will generally reduce the accuracy of such estimates. Here we show how to mitigate errors in the shadow estimation protocol recently proposed by Huang, Kueng, and Preskill. By adding an experimentally friendly calibration stage to the standard shadow estimation scheme, our robust shadow estimation algorithm can obtain an unbiased estimate of the classical shadow of a quantum system and hence extract many useful properties in a sample-efficient and noise-resilient manner given only minimal assumptions on the experimental conditions. We give rigorous bounds on the sample complexity of our protocol and demonstrate its performance with several numerical experiments.
@article{2011.09636, author = {Chen, Senrui and Yu, Wenjun and Zeng, Pei and Flammia, Steven T.}, doi = {10.1103/PRXQuantum.2.030348}, archiveprefix = {arXiv}, eprint = {2011.09636}, journal = {PRX Quantum}, pages = {030348}, title = {Robust shadow estimation}, volume = {2}, year = {2020} } -
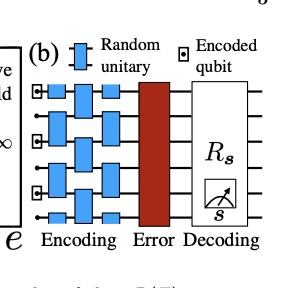 Quantum coding with low-depth random circuitsMichael J. Gullans, Stefan Krastanov, David A. Huse, Liang Jiang, and Steven T. FlammiaPhys. Rev. X, 11 031066 2021.
Quantum coding with low-depth random circuitsMichael J. Gullans, Stefan Krastanov, David A. Huse, Liang Jiang, and Steven T. FlammiaPhys. Rev. X, 11 031066 2021.Random quantum circuits have played a central role in establishing the computational advantages of near-term quantum computers over their conventional counterparts. Here, we use ensembles of low-depth random circuits with local connectivity in D≥1 spatial dimensions to generate quantum error-correcting codes. For random stabilizer codes and the erasure channel, we find strong evidence that a depth O(log N) random circuit is necessary and sufficient to converge (with high probability) to zero failure probability for any finite amount below the optimal erasure threshold, set by the channel capacity, for any D. Previous results on random circuits have only shown that O(N1/D) depth suffices or that O(log3 N) depth suffices for all-to-all connectivity (D→∞). We then study the critical behavior of the erasure threshold in the so-called moderate deviation limit, where both the failure probability and the distance to the optimal threshold converge to zero with N. We find that the requisite depth scales like O(log N) only for dimensions D≥2, and that random circuits require O(√N) depth for D=1. Finally, we introduce an "expurgation" algorithm that uses quantum measurements to remove logical operators that cause the code to fail by turning them into additional stabilizers or gauge operators. With such targeted measurements, we can achieve sub-logarithmic depth in D≥2 below capacity without increasing the maximum weight of the check operators. We find that for any rate beneath the capacity, high-performing codes with thousands of logical qubits are achievable with depth 4-8 expurgated random circuits in D=2 dimensions. These results indicate that finite-rate quantum codes are practically relevant for near-term devices and may significantly reduce the resource requirements to achieve fault tolerance for near-term applications.
@article{2010.09775, author = {Gullans, Michael J. and Krastanov, Stefan and Huse, David A. and Jiang, Liang and Flammia, Steven T.}, doi = {10.1103/PhysRevX.11.031066}, archiveprefix = {arXiv}, eprint = {2010.09775}, journal = {Phys. Rev. X}, title = {Quantum coding with low-depth random circuits}, volume = {11}, pages = {031066}, year = {2021} } -
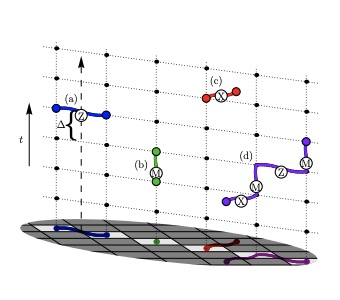 The XZZX Surface CodeJ. Pablo Bonilla Ataides, David K. Tuckett, Stephen D. Bartlett, Steven T. Flammia, and Benjamin J. BrownNat. Commun., 12 2172 2021.
The XZZX Surface CodeJ. Pablo Bonilla Ataides, David K. Tuckett, Stephen D. Bartlett, Steven T. Flammia, and Benjamin J. BrownNat. Commun., 12 2172 2021.Performing large calculations with a quantum computer will likely require a fault-tolerant architecture based on quantum error-correcting codes. The challenge is to design practical quantum error-correcting codes that perform well against realistic noise using modest resources. Here we show that a variant of the surface code – the XZZX code – offers remarkable performance for fault-tolerant quantum computation. The error threshold of this code matches what can be achieved with random codes (hashing) for every single-qubit Pauli noise channel; it is the first explicit code shown to have this universal property. We present numerical evidence that the threshold even exceeds this hashing bound for an experimentally relevant range of noise parameters. Focusing on the common situation where qubit dephasing is the dominant noise, we show that this code has a practical, high-performance decoder and surpasses all previously known thresholds in the realistic setting where syndrome measurements are unreliable. We go on to demonstrate the favourable sub-threshold resource scaling that can be obtained by specialising a code to exploit structure in the noise. We show that it is possible to maintain all of these advantages when we perform fault-tolerant quantum computation.
@article{2009.07851, author = {{Bonilla Ataides}, J. Pablo and Tuckett, David K. and Bartlett, Stephen D. and Flammia, Steven T. and Brown, Benjamin J.}, doi = {10.1038/s41467-021-22274-1}, archiveprefix = {arXiv}, eprint = {2009.07851}, journal = {Nat. Commun.}, title = {The {XZZX} Surface Code}, volume = {12}, pages = {2172}, year = {2021} } -
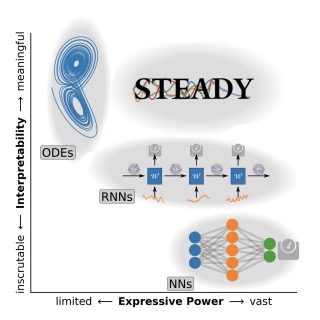 Unboxing Quantum Black Box Models: Learning Non-Markovian DynamicsStefan Krastanov, Kade Head-Marsden, Sisi Zhou, Steven T. Flammia, Liang Jiang, and Prineha NarangarXiv:2009.03902, 2020.
Unboxing Quantum Black Box Models: Learning Non-Markovian DynamicsStefan Krastanov, Kade Head-Marsden, Sisi Zhou, Steven T. Flammia, Liang Jiang, and Prineha NarangarXiv:2009.03902, 2020.Characterizing the memory properties of the environment has become critical for the high-fidelity control of qubits and other advanced quantum systems. However, current non-Markovian tomography techniques are either limited to discrete superoperators, or they employ machine learning methods, neither of which provide physical insight into the dynamics of the quantum system. To circumvent this limitation, we design learning architectures that explicitly encode physical constraints like the properties of completely-positive trace-preserving maps in a differential form. This method preserves the versatility of the machine learning approach without sacrificing the efficiency and fidelity of traditional parameter estimation methods. Our approach provides the physical interpretability that machine learning and opaque superoperators lack. Moreover, it is aware of the underlying continuous dynamics typically disregarded by superoperator-based tomography. This paradigm paves the way to noise-aware optimal quantum control and opens a path to exploiting the bath as a control and error mitigation resource.
@misc{2009.03902, doi = {10.48550/arXiv.2009.03902}, author = {Krastanov, Stefan and Head-Marsden, Kade and Zhou, Sisi and Flammia, Steven T. and Jiang, Liang and Narang, Prineha}, archiveprefix = {arXiv}, eprint = {2009.03902}, title = {Unboxing Quantum Black Box Models: Learning Non-Markovian Dynamics}, year = {2020} } -
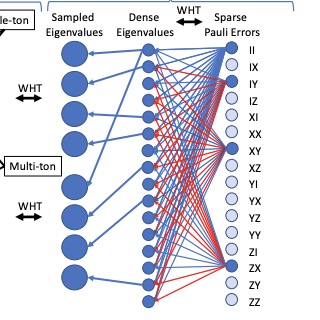 Fast Estimation of Sparse Quantum NoiseRobin Harper, Wenjun Yu, and Steven T. FlammiaPRX Quantum, 2 010322 2021.
Fast Estimation of Sparse Quantum NoiseRobin Harper, Wenjun Yu, and Steven T. FlammiaPRX Quantum, 2 010322 2021.As quantum computers approach the fault tolerance threshold, diagnosing and characterizing the noise on large scale quantum devices is increasingly important. One of the most important classes of noise channels is the class of Pauli channels, for reasons of both theoretical tractability and experimental relevance. Here we present a practical algorithm for estimating the s nonzero Pauli error rates in an s-sparse, n-qubit Pauli noise channel, or more generally the s largest Pauli error rates. The algorithm comes with rigorous recovery guarantees and uses only O(n2) measurements, O(s n2) classical processing time, and Clifford quantum circuits. We experimentally validate a heuristic version of the algorithm that uses simplified Clifford circuits on data from an IBM 14-qubit superconducting device and our open source implementation. These data show that accurate and precise estimation of the probability of arbitrary-weight Pauli errors is possible even when the signal is two orders of magnitude below the measurement noise floor.
@article{2007.07901, author = {Harper, Robin and Yu, Wenjun and Flammia, Steven T.}, doi = {10.1103/PRXQuantum.2.010322}, archiveprefix = {arXiv}, eprint = {2007.07901}, journal = {PRX Quantum}, title = {Fast Estimation of Sparse Quantum Noise}, volume = {2}, pages = {010322}, year = {2021} } -
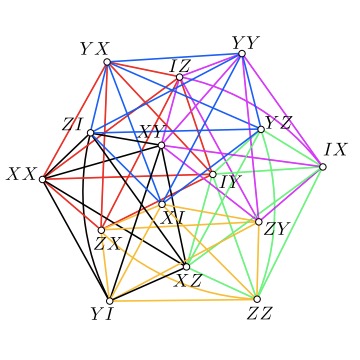 Characterization of solvable spin models via graph invariantsAdrian Chapman, and Steven T. FlammiaQuantum, 4 278 2020.
Characterization of solvable spin models via graph invariantsAdrian Chapman, and Steven T. FlammiaQuantum, 4 278 2020.Exactly solvable models are essential in physics. For many-body spin-1/2 systems, an important class of such models consists of those that can be mapped to free fermions hopping on a graph. We provide a complete characterization of models which can be solved this way. Specifically, we reduce the problem of recognizing such spin models to the graph-theoretic problem of recognizing line graphs, which has been solved optimally. A corollary of our result is a complete set of constant-sized commutation structures that constitute the obstructions to a free-fermion solution. We find that symmetries are tightly constrained in these models. Pauli symmetries correspond to either: (i) cycles on the fermion hopping graph, (ii) the fermion parity operator, or (iii) logically encoded qubits. Clifford symmetries within one of these symmetry sectors, with three exceptions, must be symmetries of the free-fermion model itself. We demonstrate how several exact free-fermion solutions from the literature fit into our formalism and give an explicit example of a new model previously unknown to be solvable by free fermions.
@article{2003.05465, author = {Chapman, Adrian and Flammia, Steven T.}, doi = {10.22331/q-2020-06-04-278}, archiveprefix = {arXiv}, eprint = {2003.05465}, journal = {Quantum}, title = {Characterization of solvable spin models via graph invariants}, volume = {4}, pages = {278}, year = {2020} } -
 Scalable Bayesian Hamiltonian learningTim J. Evans, Robin Harper, and Steven T. FlammiaarXiv:1912.07636, 2019.
Scalable Bayesian Hamiltonian learningTim J. Evans, Robin Harper, and Steven T. FlammiaarXiv:1912.07636, 2019.As the size of quantum devices continues to grow, the development of scalable methods to characterise and diagnose noise is becoming an increasingly important problem. Recent methods have shown how to efficiently estimate Hamiltonians in principle, but they are poorly conditioned and can only characterize the system up to a scalar factor, making them difficult to use in practice. In this work we present a Bayesian methodology, called Bayesian Hamiltonian Learning (BHL), that addresses both of these issues by making use of any or all, of the following: well-characterised experimental control of Hamiltonian couplings, the preparation of multiple states, and the availability of any prior information for the Hamiltonian. Importantly, BHL can be used online as an adaptive measurement protocol, updating estimates and their corresponding uncertainties as experimental data become available. In addition, we show that multiple input states and control fields enable BHL to reconstruct Hamiltonians that are neither generic nor spatially local. We demonstrate the scalability and accuracy of our method with numerical simulations on up to 100 qubits. These practical results are complemented by several theoretical contributions. We prove that a k-body Hamiltonian H whose correlation matrix has a spectral gap Δ can be estimated to precision ε with only Õ(n3k/(εΔ)3/2) measurements. We use two subroutines that may be of independent interest: First, an algorithm to approximate a steady state of H starting from an arbitrary input that converges factorially in the number of samples; and second, an algorithm to estimate the expectation values of m Pauli operators with weight ≤k to precision ϵ using only O(ϵ−2 3k log m) measurements, which quadratically improves a recent result by Cotler and Wilczek.
@misc{1912.07636, doi = {10.48550/arXiv.1912.07636}, author = {Evans, Tim J. and Harper, Robin and Flammia, Steven T.}, archiveprefix = {arXiv}, eprint = {1912.07636}, title = {Scalable {B}ayesian {H}amiltonian learning}, year = {2019} } -
 Efficient learning of quantum noiseRobin Harper, Steven T. Flammia, and Joel J. WallmanNature Physics, 16 1184–1188 2020.
Efficient learning of quantum noiseRobin Harper, Steven T. Flammia, and Joel J. WallmanNature Physics, 16 1184–1188 2020.Noise is the central obstacle to building large-scale quantum computers. Quantum systems with sufficiently uncorrelated and weak noise could be used to solve computational problems that are intractable with current digital computers. There has been substantial progress towards engineering such systems. However, continued progress depends on the ability to characterize quantum noise reliably and efficiently with high precision. Here we describe such a protocol and report its experimental implementation on a 14-qubit superconducting quantum architecture. The method returns an estimate of the effective noise and can detect correlations within arbitrary sets of qubits. We show how to construct a quantum noise correlation matrix allowing the easy visualization of correlations between all pairs of qubits, enabling the discovery of long-range two-qubit correlations in the 14 qubit device that had not previously been detected. Our results are the first implementation of a provably rigorous and comprehensive diagnostic protocol capable of being run on state of the art devices and beyond. These results pave the way for noise metrology in next-generation quantum devices, calibration in the presence of crosstalk, bespoke quantum error-correcting codes, and customized fault-tolerance protocols that can greatly reduce the overhead in a quantum computation.
@article{1907.13022, author = {Harper, Robin and Flammia, Steven T. and Wallman, Joel J.}, doi = {10.1038/s41567-020-0992-8}, archiveprefix = {arXiv}, eprint = {1907.13022}, journal = {Nature Physics}, title = {Efficient learning of quantum noise}, volume = {16}, pages = {1184--1188}, year = {2020} } -
 Efficient estimation of Pauli channelsSteven T. Flammia, and Joel J. WallmanACM Transactions on Quantum Computing, 1 1–32 2020.
Efficient estimation of Pauli channelsSteven T. Flammia, and Joel J. WallmanACM Transactions on Quantum Computing, 1 1–32 2020.Pauli channels are ubiquitous in quantum information, both as a dominant noise source in many computing architectures and as a practical model for analyzing error correction and fault tolerance. Here we prove several results on efficiently learning Pauli channels, and more generally the Pauli projection of a quantum channel. We first derive a procedure for learning a Pauli channel on n qubits with high probability to a relative precision ϵ using O(ϵ−2 n 2n) measurements, which is efficient in the Hilbert space dimension. The estimate is robust to state preparation and measurement errors which, together with the relative precision, makes it especially appropriate for applications involving characterization of high-accuracy quantum gates. Next we show that the error rates for an arbitrary set of s Pauli errors can be estimated to a relative precision ϵ using O(ϵ−4 log s log s/ϵ) measurements. Finally, we show that when the Pauli channel is given by a Markov field with at most k-local correlations, we can learn an entire n-qubit Pauli channel to relative precision ϵ with only Ok(ϵ−2 n2 log n) measurements, which is efficient in the number of qubits. These results enable a host of applications beyond just characterizing noise in a large-scale quantum system: they pave the way to tailoring quantum codes, optimizing decoders, and customizing fault tolerance procedures to suit a particular device.
@article{1907.12976, author = {Flammia, Steven T. and Wallman, Joel J.}, doi = {10.1145/3408039}, archiveprefix = {arXiv}, eprint = {1907.12976}, journal = {ACM Transactions on Quantum Computing}, title = {Efficient estimation of {P}auli channels}, volume = {1}, pages = {1--32}, year = {2020} } -
 Fault-tolerant thresholds for the surface code in excess of 5% under biased noiseDavid K. Tuckett, Stephen D. Bartlett, Steven T. Flammia, and Benjamin J. BrownPhys. Rev. Lett., 124 130501 2020.
Fault-tolerant thresholds for the surface code in excess of 5% under biased noiseDavid K. Tuckett, Stephen D. Bartlett, Steven T. Flammia, and Benjamin J. BrownPhys. Rev. Lett., 124 130501 2020.Noise in quantum computing is countered with quantum error correction. Achieving optimal performance will require tailoring codes and decoding algorithms to account for features of realistic noise, such as the common situation where the noise is biased towards dephasing. Here we introduce an efficient high-threshold decoder for a noise-tailored surface code based on minimum-weight perfect matching. The decoder exploits the symmetries of its syndrome under the action of biased noise and generalises to the fault-tolerant regime where measurements are unreliable. Using this decoder, we obtain fault-tolerant thresholds in excess of 6% for a phenomenological noise model in the limit where dephasing dominates. These gains persist even for modest noise biases: we find a threshold of ∼5% in an experimentally relevant regime where dephasing errors occur at a rate one hundred times greater than bit-flip errors.
@article{1907.02554, author = {Tuckett, David K. and Bartlett, Stephen D. and Flammia, Steven T. and Brown, Benjamin J.}, doi = {10.1103/PhysRevLett.124.130501}, archiveprefix = {arXiv}, eprint = {1907.02554}, journal = {Phys. Rev. Lett.}, title = {Fault-tolerant thresholds for the surface code in excess of 5\% under biased noise}, volume = {124}, pages = {130501}, year = {2020} } -
 Bias-preserving gates with stabilized cat qubitsShruti Puri, Lucas St-Jean, Jonathan A. Gross, Alexander Grimm, N. E. Frattini, Pavithran S. Iyer, Anirudh Krishna, Steven Touzard, Liang Jiang, Alexandre Blais, and 2 more authorsScience Advances, 6 130501 2020.
Bias-preserving gates with stabilized cat qubitsShruti Puri, Lucas St-Jean, Jonathan A. Gross, Alexander Grimm, N. E. Frattini, Pavithran S. Iyer, Anirudh Krishna, Steven Touzard, Liang Jiang, Alexandre Blais, and 2 more authorsScience Advances, 6 130501 2020.The code capacity threshold for error correction using qubits which exhibit asymmetric or biased noise channels is known to be much higher than with qubits without such structured noise. However, it is unclear how much this improvement persists when realistic circuit level noise is taken into account. This is because implementations of gates which do not commute with the dominant error un-bias the noise channel. In particular, a native bias-preserving controlled-NOT (CX) gate, which is an essential ingredient of stabilizer codes, is not possible in strictly two-level systems. Here we overcome the challenge of implementing a bias-preserving CX gate by using stabilized cat qubits in driven nonlinear oscillators. The physical noise channel of this qubit is biased towards phase-flips, which increase linearly with the size of the cat, while bit-flips are exponentially suppressed with cat size. Remarkably, the error channel of this native CX gate between two such cat qubits is also dominated by phase-flips, while bit-flips remain exponentially suppressed. This CX gate relies on the topological phase that arises from the rotation of the cat qubit in phase space. The availability of bias-preserving CX gates opens a path towards fault-tolerant codes tailored to biased-noise cat qubits with high threshold and low overhead. As an example, we analyze a scheme for concatenated error correction using cat qubits. We find that the availability of CX gates with moderately sized cat qubits, having mean photon number <10, improves a rigorous lower bound on the fault-tolerance threshold by a factor of two and decreases the overhead in logical Clifford operations by a factor of 5. We expect these estimates to improve significantly with further optimization and with direct use of other codes such as topological codes tailored to biased noise.
@article{1905.00450, author = {Puri, Shruti and St-Jean, Lucas and Gross, Jonathan A. and Grimm, Alexander and Frattini, N. E. and Iyer, Pavithran S. and Krishna, Anirudh and Touzard, Steven and Jiang, Liang and Blais, Alexandre and Flammia, Steven T. and Girvin, S. M.}, doi = {10.1126/sciadv.aay5901}, archiveprefix = {arXiv}, eprint = {1905.00450}, journal = {Science Advances}, number = {34}, title = {Bias-preserving gates with stabilized cat qubits}, volume = {6}, year = {2020} } -
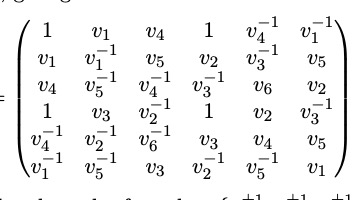 Tight Frames, Hadamard Matrices and Zauner’s ConjectureMarcus Appleby, Ingemar Bengtsson, Steven Flammia, and Dardo GoyenecheJ. Phys. A, 52 295301 2019.
Tight Frames, Hadamard Matrices and Zauner’s ConjectureMarcus Appleby, Ingemar Bengtsson, Steven Flammia, and Dardo GoyenecheJ. Phys. A, 52 295301 2019.We show that naturally associated to a SIC (symmetric informationally complete positive operator valued measure or SIC-POVM) in dimension d there are a number of higher dimensional structures: specifically a projector and a complex Hadamard matrix in dimension d squared and a pair of ETFs (equiangular tight frames) in dimensions d(d-1)/2, d(d+1)/2. We also show that a WH (Weyl Heisenberg covariant) SIC in odd dimension d is naturally associated to a pair of symmetric tight fusion frames in dimension d. We deduce two relaxations of the WH SIC existence problem. We also find a reformulation of the problem in which the number of equations is fewer than the number of variables. Finally, we show that in at least four cases the structures associated to a SIC lie on continuous manifolds of such structures. In two of these cases the manifolds are non-linear. Restricted defect calculations are consistent with this being true for the structures associated to every known SIC with d between 3 and 16, suggesting it may be true for all d greater than 2.
@article{1903.06721, author = {Appleby, Marcus and Bengtsson, Ingemar and Flammia, Steven and Goyeneche, Dardo}, doi = {10.1088/1751-8121/ab25ad}, archiveprefix = {arXiv}, eprint = {1903.06721}, journal = {J. Phys. A}, title = {Tight Frames, {H}adamard Matrices and {Z}auner's Conjecture}, volume = {52}, pages = {295301}, year = {2019} } -
 Statistical analysis of randomized benchmarkingRobin Harper, Ian Hincks, Chris Ferrie, Steven T. Flammia, and Joel J. WallmanPhys. Rev. A, 99 052350 2019.
Statistical analysis of randomized benchmarkingRobin Harper, Ian Hincks, Chris Ferrie, Steven T. Flammia, and Joel J. WallmanPhys. Rev. A, 99 052350 2019.Randomized benchmarking and variants thereof, which we collectively call RB+, are widely used to characterize the performance of quantum computers because they are simple, scalable, and robust to state-preparation and measurement errors. However, experimental implementations of RB+ allocate resources suboptimally and make ad-hoc assumptions that undermine the reliability of the data analysis. In this paper, we propose a simple modification of RB+ which rigorously eliminates a nuisance parameter and simplifies the experimental design. We then show that, with this modification and specific experimental choices, RB+ efficiently provides estimates of error rates with multiplicative precision. Finally, we provide a simplified rigorous method for obtaining credible regions for parameters of interest and a heuristic approximation for these intervals that performs well in currently relevant regimes.
@article{1901.00535, author = {Harper, Robin and Hincks, Ian and Ferrie, Chris and Flammia, Steven T. and Wallman, Joel J.}, doi = {10.1103/PhysRevA.99.052350}, archiveprefix = {arXiv}, eprint = {1901.00535}, journal = {Phys. Rev. A}, title = {Statistical analysis of randomized benchmarking}, volume = {99}, pages = {052350}, year = {2019} } -
 Tailoring surface codes for highly biased noiseDavid K. Tuckett, Andrew S. Darmawan, Christopher T. Chubb, Sergey Bravyi, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. X, 9 041031 2018.
Tailoring surface codes for highly biased noiseDavid K. Tuckett, Andrew S. Darmawan, Christopher T. Chubb, Sergey Bravyi, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. X, 9 041031 2018.The surface code, with a simple modification, exhibits ultra-high error correction thresholds when the noise is biased towards dephasing. Here, we identify features of the surface code responsible for these ultra-high thresholds. We provide strong evidence that the threshold error rate of the surface code tracks the hashing bound exactly for all biases, and show how to exploit these features to achieve significant improvement in logical failure rate. First, we consider the infinite bias limit, meaning pure dephasing. We prove that the error threshold of the modified surface code for pure dephasing noise is 50%, i.e., that all qubits are fully dephased, and this threshold can be achieved by a polynomial time decoding algorithm. We demonstrate that the sub-threshold behavior of the code depends critically on the precise shape and boundary conditions of the code. That is, for rectangular surface codes with standard rough/smooth open boundaries, it is controlled by the parameter g=gcd(j,k), where j and k are dimensions of the surface code lattice. We demonstrate a significant improvement in logical failure rate with pure dephasing for co-prime codes that have g=1, and closely-related rotated codes, which have a modified boundary. The effect is dramatic: the same logical failure rate achievable with a square surface code and n physical qubits can be obtained with a co-prime or rotated surface code using only O(√n) physical qubits. Finally, we use approximate maximum likelihood decoding to demonstrate that this improvement persists for a general Pauli noise biased towards dephasing. In particular, comparing with a square surface code, we observe a significant improvement in logical failure rate against biased noise using a rotated surface code with approximately half the number of physical qubits.
@article{1812.08186, author = {Tuckett, David K. and Darmawan, Andrew S. and Chubb, Christopher T. and Bravyi, Sergey and Bartlett, Stephen D. and Flammia, Steven T.}, doi = {10.1103/PhysRevX.9.041031}, archiveprefix = {arXiv}, eprint = {1812.08186}, journal = {Phys. Rev. X}, title = {Tailoring surface codes for highly biased noise}, volume = {9}, pages = {041031}, year = {2018} } -
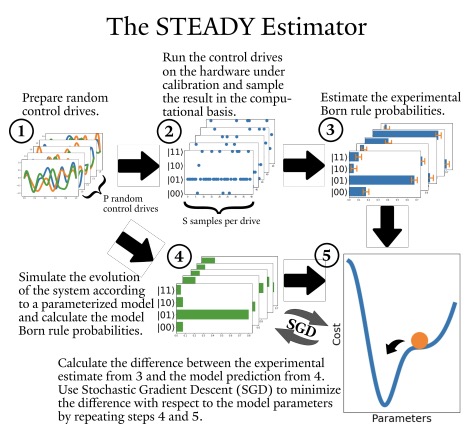 Stochastic Estimation of Dynamical VariablesStefan Krastanov, Sisi Zhou, Steven T. Flammia, and Liang JiangQuantum Science and Technology, 4 035003 2019.
Stochastic Estimation of Dynamical VariablesStefan Krastanov, Sisi Zhou, Steven T. Flammia, and Liang JiangQuantum Science and Technology, 4 035003 2019.Estimating the parameters governing the dynamics of a system is a prerequisite for its optimal control. We present a simple but powerful method that we call STEADY, for STochastic Estimation algorithm for DYnamical variables, to estimate the Hamiltonian (or Lindbladian) governing a quantum system of a few qubits. STEADY makes efficient use of all measurements and its performance scales as the information-theoretic limits for such an estimator. Importantly, it is inherently robust to state preparation and measurement errors. It is not limited to evaluating only a fixed set of possible gates, rather it estimates the complete Hamiltonian of the system. The estimator is applicable to any Hamiltonian that can be written as a piecewise-differentiable function and it can easily include estimators for the non-unitary parameters as well. At the heart of our approach is a stochastic gradient descent over the difference between experimental measurement and model prediction.
@article{1812.05120, author = {Krastanov, Stefan and Zhou, Sisi and Flammia, Steven T. and Jiang, Liang}, doi = {10.1088/2058-9565/ab18d5}, archiveprefix = {arXiv}, eprint = {1812.05120}, journal = {Quantum Science and Technology}, title = {Stochastic Estimation of Dynamical Variables}, volume = {4}, pages = {035003}, year = {2019} } -
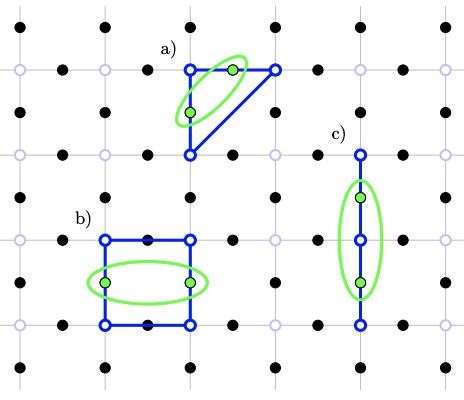 Statistical mechanical models for quantum codes with correlated noiseChristopher T. Chubb, and Steven T. FlammiaAnnales de L’Institut Henri Poincaré D, 8 269–321 2021.
Statistical mechanical models for quantum codes with correlated noiseChristopher T. Chubb, and Steven T. FlammiaAnnales de L’Institut Henri Poincaré D, 8 269–321 2021.We give a broad generalisation of the mapping, originally due to Dennis, Kitaev, Landahl and Preskill, from quantum error correcting codes to statistical mechanical models. We show how the mapping can be extended to arbitrary stabiliser or subsystem codes subject to correlated Pauli noise models, including models of fault tolerance. This mapping connects the error correction threshold of the quantum code to a phase transition in the statistical mechanical model. Thus, any existing method for finding phase transitions, such as Monte Carlo simulations, can be applied to approximate the threshold of any such code, without having to perform optimal decoding. By way of example, we numerically study the threshold of the surface code under mildly correlated bit-flip noise, showing that noise with bunching correlations causes the threshold to drop to pcorr=10.04(6)%, from its known iid value of piid=10.917(3)%. Complementing this, we show that the mapping also allows us to utilise any algorithm which can calculate/approximate partition functions of classical statistical mechanical models to perform optimal/approximately optimal decoding. Specifically, for 2D codes subject to locally correlated noise, we give a linear-time tensor network-based algorithm for approximate optimal decoding which extends the MPS decoder of Bravyi, Suchara and Vargo.
@article{1809.10704, author = {Chubb, Christopher T. and Flammia, Steven T.}, doi = {10.4171/AIHPD/105}, archiveprefix = {arXiv}, eprint = {1809.10704}, journal = {Annales de L'Institut Henri Poincar\'e D}, title = {Statistical mechanical models for quantum codes with correlated noise}, volume = {8}, pages = {269--321}, year = {2021} } -
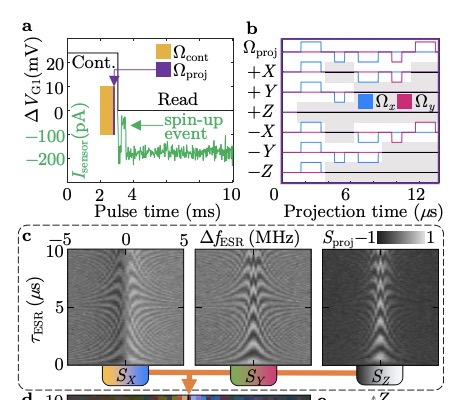 Silicon qubit fidelities approaching incoherent noise limits via pulse engineeringC. H. Yang, K. W. Chan, R. Harper, W. Huang, T. Evans, J. C. C. Hwang, B. Hensen, A. Laucht, T. Tanttu, F. E. Hudson, and 5 more authorsNature Electronics, 2 151–158 2019.
Silicon qubit fidelities approaching incoherent noise limits via pulse engineeringC. H. Yang, K. W. Chan, R. Harper, W. Huang, T. Evans, J. C. C. Hwang, B. Hensen, A. Laucht, T. Tanttu, F. E. Hudson, and 5 more authorsNature Electronics, 2 151–158 2019.The performance requirements for fault-tolerant quantum computing are very stringent. Qubits must be manipulated, coupled, and measured with error rates well below 1%. For semiconductor implementations, silicon quantum dot spin qubits have demonstrated average single-qubit Clifford gate error rates that approach this threshold, notably with error rates of 0.14% in isotopically enriched 28Si/SiGe devices. This gate performance, together with high-fidelity two-qubit gates and measurements, is only known to meet the threshold for fault-tolerant quantum computing in some architectures when assuming that the noise is incoherent, and still lower error rates are needed to reduce overhead. Here we experimentally show that pulse engineering techniques, widely used in magnetic resonance, improve average Clifford gate error rates for silicon quantum dot spin qubits to 0.043%,a factor of 3 improvement on previous best results for silicon quantum dot devices. By including tomographically complete measurements in randomised benchmarking, we infer a higher-order feature of the noise called the unitarity, which measures the coherence of noise. This in turn allows us to theoretically predict that average gate error rates as low as 0.026% may be achievable with further pulse improvements. These fidelities are ultimately limited by Markovian noise, which we attribute to charge noise emanating from the silicon device structure itself, or the environment.
@article{1807.09500, author = {Yang, C. H. and Chan, K. W. and Harper, R. and Huang, W. and Evans, T. and Hwang, J. C. C. and Hensen, B. and Laucht, A. and Tanttu, T. and Hudson, F. E. and Flammia, S. T. and Itoh, K. M. and Morello, A. and Bartlett, S. D. and Dzurak, A. S.}, doi = {10.1038/s41928-019-0234-1}, archiveprefix = {arXiv}, eprint = {1807.09500}, journal = {Nature Electronics}, title = {Silicon qubit fidelities approaching incoherent noise limits via pulse engineering}, volume = {2}, pages = {151--158}, year = {2019} } -
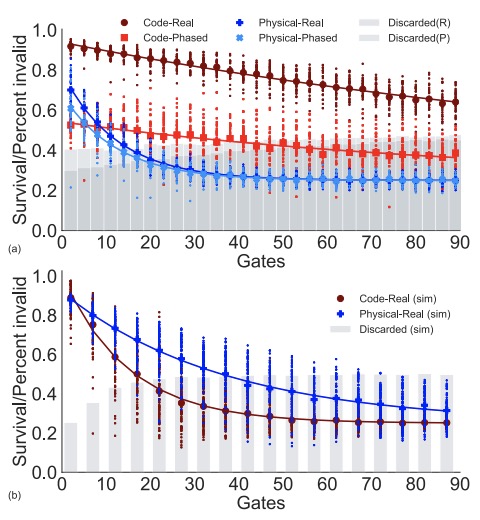 Fault-Tolerant Logical Gates in the IBM Quantum ExperienceRobin Harper, and Steven T. FlammiaPhys. Rev. Lett., 122 080504 2019.
Fault-Tolerant Logical Gates in the IBM Quantum ExperienceRobin Harper, and Steven T. FlammiaPhys. Rev. Lett., 122 080504 2019.Quantum computers will require encoding of quantum information to protect them from noise. Fault-tolerant quantum computing architectures illustrate how this might be done but have not yet shown a conclusive practical advantage. Here we demonstrate that a small but useful error detecting code improves the fidelity of the fault-tolerant gates implemented in the code space as compared to the fidelity of physically equivalent gates implemented on physical qubits. By running a randomized benchmarking protocol in the logical code space of the [4,2,2] code, we observe an order of magnitude improvement in the infidelity of the gates, with the two-qubit infidelity dropping from 5.8(2)% to 0.60(3)%. Our results are consistent with fault-tolerance theory and conclusively demonstrate the benefit of carrying out computation in a code space that can detect errors. Although the fault-tolerant gates offer an impressive improvement in fidelity, the computation as a whole is not below the fault-tolerance threshold because of noise associated with state preparation and measurement on this device.
@article{1806.02359, author = {Harper, Robin and Flammia, Steven T.}, doi = {10.1103/PhysRevLett.122.080504}, archiveprefix = {arXiv}, eprint = {1806.02359}, journal = {Phys. Rev. Lett.}, title = {Fault-Tolerant Logical Gates in the {IBM} {Q}uantum {E}xperience}, volume = {122}, pages = {080504}, year = {2019} } -
 Performance of quantum error correction with coherent errorsEric Huang, Andrew C. Doherty, and Steven FlammiaPhys. Rev. A, 99 022313 2019.
Performance of quantum error correction with coherent errorsEric Huang, Andrew C. Doherty, and Steven FlammiaPhys. Rev. A, 99 022313 2019.We compare the performance of quantum error correcting codes when memory errors are unitary with the more familiar case of dephasing noise. For a wide range of codes we analytically compute the effective logical channel that results when the error correction steps are performed noiselessly. Our examples include the entire family of repetition codes, the 5-qubit, Steane, Shor, and surface codes. When errors are measured in terms of the diamond norm, we find that the error correction is typically much more effective for unitary errors than for dephasing. We observe this behavior for a wide range of codes after a single level of encoding, and in the thresholds of concatenated codes using hard decoders. We show that this holds with great generality by proving a bound on the performance of any stabilizer code when the noise at the physical level is unitary. By comparing the diamond norm error D′ of the logical qubit with the same quantity at the physical level D, we show that D′≤cDd where d is the distance of the code and c is constant that depends on the code but not on the error. This bound compares very favorably to the performance of error correction for dephasing noise and other Pauli channels, where an error correcting code of odd distance d will exhibit a scaling D′∼D(d+1)/2.
@article{1805.08227, author = {Huang, Eric and Doherty, Andrew C. and Flammia, Steven}, doi = {10.1103/PhysRevA.99.022313}, archiveprefix = {arXiv}, eprint = {1805.08227}, journal = {Phys. Rev. A}, title = {Performance of quantum error correction with coherent errors}, volume = {99}, pages = {022313}, year = {2019} } -
 Real Randomized BenchmarkingA. K. Hashagen, S. T. Flammia, D. Gross, and J. J. WallmanQuantum, 2 85 2018.
Real Randomized BenchmarkingA. K. Hashagen, S. T. Flammia, D. Gross, and J. J. WallmanQuantum, 2 85 2018.Randomized benchmarking provides a tool for obtaining precise quantitative estimates of the average error rate of a physical quantum channel. Here we define real randomized benchmarking, which enables a separate determination of the average error rate in the real and complex parts of the channel. This provides more fine-grained information about average error rates with approximately the same cost as the standard protocol. The protocol requires only averaging over the real Clifford group, a subgroup of the full complex Clifford group, and makes use of the fact that it forms an orthogonal 2-design. It therefore allows benchmarking of fault-tolerant gates for an encoding which does not contain the full Clifford group transversally. Furthermore, our results are especially useful when considering quantum computations on rebits (or real encodings of complex computations), in which case the real Clifford group now plays the role of the complex Clifford group when studying stabilizer circuits.
@article{1801.06121, author = {Hashagen, A. K. and Flammia, S. T. and Gross, D. and Wallman, J. J.}, doi = {10.22331/q-2018-08-22-85}, archiveprefix = {arXiv}, eprint = {1801.06121}, journal = {Quantum}, title = {Real Randomized Benchmarking}, volume = {2}, pages = {85}, year = {2018} } -
 Ultrahigh Error Threshold for Surface Codes with Biased NoiseDavid K. Tuckett, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. Lett., 120 050505 2018.
Ultrahigh Error Threshold for Surface Codes with Biased NoiseDavid K. Tuckett, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. Lett., 120 050505 2018.We show that a simple modification of the surface code can exhibit an enormous gain in the error correction threshold for a noise model in which Pauli Z errors occur more frequently than X or Y errors. Such biased noise, where dephasing dominates, is ubiquitous in many quantum architectures. In the limit of pure dephasing noise we find a threshold of 43.7(1)% using a tensor network decoder proposed by Bravyi, Suchara and Vargo. The threshold remains surprisingly large in the regime of realistic noise bias ratios, for example 28.2(2)% at a bias of 10. The performance is in fact at or near the hashing bound for all values of the bias. The modified surface code still uses only weight-4 stabilizers on a square lattice, but merely requires measuring products of Y instead of Z around the faces, as this doubles the number of useful syndrome bits associated with the dominant Z errors. Our results demonstrate that large efficiency gains can be found by appropriately tailoring codes and decoders to realistic noise models, even under the locality constraints of topological codes.
@article{1708.08474, author = {Tuckett, David K. and Bartlett, Stephen D. and Flammia, Steven T.}, doi = {10.1103/PhysRevLett.120.050505}, archiveprefix = {arXiv}, eprint = {1708.08474}, journal = {Phys. Rev. Lett.}, title = {Ultrahigh Error Threshold for Surface Codes with Biased Noise}, volume = {120}, pages = {050505}, year = {2018} } -
 Dimension towers of SICs. I. Aligned SICs and embedded tight framesMarcus Appleby, Ingemar Bengtsson, Irina Dumitru, and Steven FlammiaJ. Math. Phys., 58 122201 2017.
Dimension towers of SICs. I. Aligned SICs and embedded tight framesMarcus Appleby, Ingemar Bengtsson, Irina Dumitru, and Steven FlammiaJ. Math. Phys., 58 122201 2017.Algebraic number theory relates SIC-POVMs in dimension d>3 to those in dimension d(d−2). We define a SIC in dimension d(d−2) to be aligned to a SIC in dimension d if and only if the squares of the overlap phases in dimension d appear as a subset of the overlap phases in dimension d(d−2) in a specified way. We give 19 (mostly numerical) examples of aligned SICs. We conjecture that given any SIC in dimension d there exists an aligned SIC in dimension d(d−2). In all our examples the aligned SIC has lower dimensional equiangular tight frames embedded in it. If d is odd so that a natural tensor product structure exists, we prove that the individual vectors in the aligned SIC have a very special entanglement structure, and the existence of the embedded tight frames follows as a theorem. If d−2 is an odd prime number we prove that a complete set of mutually unbiased bases can be obtained by reducing an aligned SIC to this dimension.
@article{1707.09911, author = {Appleby, Marcus and Bengtsson, Ingemar and Dumitru, Irina and Flammia, Steven}, doi = {10.1063/1.4999844}, archiveprefix = {arXiv}, eprint = {1707.09911}, journal = {J. Math. Phys.}, title = {Dimension towers of {SIC}s. {I}. Aligned {SIC}s and embedded tight frames}, volume = {58}, pages = {122201}, year = {2017} } -
 Topological quantum error correction in the Kitaev honeycomb modelYi-Chan Lee, Courtney Brell, and Steven T. FlammiaJournal of Statistical Mechanics: Theory and Experiment, 2017 083106 2017.
Topological quantum error correction in the Kitaev honeycomb modelYi-Chan Lee, Courtney Brell, and Steven T. FlammiaJournal of Statistical Mechanics: Theory and Experiment, 2017 083106 2017.The Kitaev honeycomb model is an approximate topological quantum error correcting code in the same phase as the toric code, but requiring only a 2-body Hamiltonian. As a frustrated spin model, it is well outside the commuting models of topological quantum codes that are typically studied, but its exact solubility makes it more amenable to analysis of effects arising in this noncommutative setting than a generic topologically ordered Hamiltonian. Here we study quantum error correction in the honeycomb model using both analytic and numerical techniques. We first prove explicit exponential bounds on the approximate degeneracy, local indistinguishability, and correctability of the code space. These bounds are tighter than can be achieved using known general properties of topological phases. Our proofs are specialized to the honeycomb model, but some of the methods may nonetheless be of broader interest. Following this, we numerically study noise caused by thermalization processes in the perturbative regime close to the toric code renormalization group fixed point. The appearance of non-topological excitations in this setting has no significant effect on the error correction properties of the honeycomb model in the regimes we study. Although the behavior of this model is found to be qualitatively similar to that of the standard toric code in most regimes, we find numerical evidence of an interesting effect in the low-temperature, finite-size regime where a preferred lattice direction emerges and anyon diffusion is geometrically constrained. We expect this effect to yield an improvement in the scaling of the lifetime with system size as compared to the standard toric code.
@article{1705.01563, author = {Lee, Yi-Chan and Brell, Courtney and Flammia, Steven T.}, doi = {10.1088/1742-5468/aa7ee2}, archiveprefix = {arXiv}, eprint = {1705.01563}, journal = {Journal of Statistical Mechanics: Theory and Experiment}, title = {Topological quantum error correction in the {K}itaev honeycomb model}, volume = {2017}, pages = {083106}, year = {2017} } -
 Beating the Classical Limits of Information Transmission using a Quantum DecoderRobert J. Chapman, Akib Karim, Zixin Huang, Steven T. Flammia, Marco Tomamichel, and Alberto PeruzzoPhys. Rev. A, 97 012315 2018.
Beating the Classical Limits of Information Transmission using a Quantum DecoderRobert J. Chapman, Akib Karim, Zixin Huang, Steven T. Flammia, Marco Tomamichel, and Alberto PeruzzoPhys. Rev. A, 97 012315 2018.Encoding schemes and error-correcting codes are widely used in information technology to improve the reliability of data transmission over real-world communication channels. Quantum information protocols can further enhance the performance in data transmission by encoding a message in quantum states, however, most proposals to date have focused on the regime of a large number of uses of the noisy channel, which is unfeasible with current quantum technology. We experimentally demonstrate quantum enhanced communication over an amplitude damping noisy channel with only two uses of the channel per bit and a single entangling gate at the decoder. By simulating the channel using a photonic interferometric setup, we experimentally increase the reliability of transmitting a data bit by greater than 20% for a certain damping range over classically sending the message twice. We show how our methodology can be extended to larger systems by simulating the transmission of a single bit with up to eight uses of the channel and a two-bit message with three uses of the channel, predicting a quantum enhancement in all cases.
@article{1704.07036, author = {Chapman, Robert J. and Karim, Akib and Huang, Zixin and Flammia, Steven T. and Tomamichel, Marco and Peruzzo, Alberto}, doi = {10.1103/PhysRevA.97.012315}, archiveprefix = {arXiv}, eprint = {1704.07036}, journal = {Phys. Rev. A}, title = {Beating the Classical Limits of Information Transmission using a Quantum Decoder}, volume = {97}, pages = {012315}, year = {2018} } -
 Tailored codes for small quantum memoriesAlan Robertson, Christopher Granade, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. Applied, 8 064004 2017.
Tailored codes for small quantum memoriesAlan Robertson, Christopher Granade, Stephen D. Bartlett, and Steven T. FlammiaPhys. Rev. Applied, 8 064004 2017.We demonstrate that small quantum memories, realized via quantum error correction in multi-qubit devices, can benefit substantially by choosing a quantum code that is tailored to the relevant error model of the system. For a biased noise model, with independent bit and phase flips occurring at different rates, we show that a single code greatly outperforms the well-studied Steane code across the full range of parameters of the noise model, including for unbiased noise. In fact, this tailored code performs almost optimally when compared with 10,000 randomly selected stabilizer codes of comparable experimental complexity. Tailored codes can even outperform the Steane code with realistic experimental noise, and without any increase in the experimental complexity, as we demonstrate by comparison in the observed error model in a recent 7-qubit trapped ion experiment.
@article{1703.08179, author = {Robertson, Alan and Granade, Christopher and Bartlett, Stephen D. and Flammia, Steven T.}, doi = {10.1103/PhysRevApplied.8.064004}, archiveprefix = {arXiv}, eprint = {1703.08179}, journal = {Phys. Rev. Applied}, title = {Tailored codes for small quantum memories}, volume = {8}, pages = {064004}, year = {2017} } -
 Constructing exact symmetric informationally complete measurements from numerical solutionsMarcus Appleby, Tuan-Yow Chien, Steven Flammia, and Shayne WaldronJ. Phys. A, 51 165302 2018.
Constructing exact symmetric informationally complete measurements from numerical solutionsMarcus Appleby, Tuan-Yow Chien, Steven Flammia, and Shayne WaldronJ. Phys. A, 51 165302 2018.Recently, several intriguing conjectures have been proposed connecting symmetric informationally complete quantum measurements (SIC POVMs, or SICs) and algebraic number theory. These conjectures relate the SICs and their minimal defining algebraic number field. Testing or sharpening these conjectures requires that the SICs are expressed exactly, rather than as numerical approximations. While many exact solutions of SICs have been constructed previously using Gröbner bases, this method has probably been taken as far as is possible with current computer technology (except in special cases where there are additional symmetries). Here we describe a method for converting high-precision numerical solutions into exact ones using an integer relation algorithm in conjunction with the Galois symmetries of a SIC. Using this method we have calculated 69 new exact solutions, including 9 new dimensions where previously only numerical solutions were known, which more than triples the number of known exact solutions. In some cases the solutions require number fields with degrees as high as 12,288. We use these solutions to confirm that they obey the number-theoretic conjectures and we address two questions suggested by the previous work.
@article{1703.05981, author = {Appleby, Marcus and Chien, Tuan-Yow and Flammia, Steven and Waldron, Shayne}, doi = {10.1088/1751-8121/aab4cd}, archiveprefix = {arXiv}, eprint = {1703.05981}, journal = {J. Phys. A}, title = {Constructing exact symmetric informationally complete measurements from numerical solutions}, volume = {51}, pages = {165302}, year = {2018} } -
 Logical Randomized BenchmarkingJoshua Combes, Christopher Granade, Christopher Ferrie, and Steven T. FlammiaarXiv:1702.03688, 2017.
Logical Randomized BenchmarkingJoshua Combes, Christopher Granade, Christopher Ferrie, and Steven T. FlammiaarXiv:1702.03688, 2017.Extrapolating physical error rates to logical error rates requires many assumptions and thus can radically under- or overestimate the performance of an error correction implementation. We introduce logical randomized benchmarking, a characterization procedure that directly assesses the performance of a quantum error correction implementation at the logical level, and is motivated by a reduction to the well-studied case of physical randomized benchmarking. We show that our method reliably reports logical performance and can estimate the average probability of correctable and uncorrectable errors for a given code and physical channel.
@misc{1702.03688, doi = {10.48550/arXiv.1702.03688}, author = {Combes, Joshua and Granade, Christopher and Ferrie, Christopher and Flammia, Steven T.}, archiveprefix = {arXiv}, eprint = {1702.03688}, title = {Logical Randomized Benchmarking}, year = {2017} } -
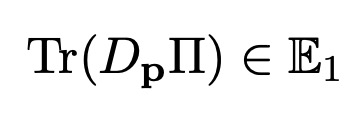 SICs and Algebraic Number TheoryMarcus Appleby, Steven Flammia, Gary McConnell, and Jon YardFound. Phys., 47 1042–1059 2017.
SICs and Algebraic Number TheoryMarcus Appleby, Steven Flammia, Gary McConnell, and Jon YardFound. Phys., 47 1042–1059 2017.We give an overview of some remarkable connections between symmetric informationally complete measurements (SIC-POVMs, or SICs) and algebraic number theory, in particular, a connection with Hilbert’s 12th problem. The paper is meant to be intelligible to a physicist who has no prior knowledge of either Galois theory or algebraic number theory.
@article{1701.05200, author = {Appleby, Marcus and Flammia, Steven and McConnell, Gary and Yard, Jon}, doi = {10.1007/s10701-017-0090-7}, archiveprefix = {arXiv}, eprint = {1701.05200}, journal = {Found. Phys.}, title = {{SIC}s and Algebraic Number Theory}, volume = {47}, pages = {1042--1059}, year = {2017} } -
 Multi-qubit Randomized Benchmarking Using Few SamplesJonas Helsen, Joel J. Wallman, Steven T. Flammia, and Stephanie WehnerPhys. Rev. A, 100 032304 2019.
Multi-qubit Randomized Benchmarking Using Few SamplesJonas Helsen, Joel J. Wallman, Steven T. Flammia, and Stephanie WehnerPhys. Rev. A, 100 032304 2019.Randomized benchmarking (RB) is an efficient and robust method to characterize gate errors in quantum circuits. Averaging over random sequences of gates leads to estimates of gate errors in terms of the average fidelity. These estimates are isolated from the state preparation and measurement errors that plague other methods like channel tomography and direct fidelity estimation. A decisive factor in the feasibility of randomized benchmarking is the number of sampled sequences required to obtain rigorous confidence intervals. Previous bounds were either prohibitively loose or required the number of sampled sequences to scale exponentially with the number of qubits in order to obtain a fixed confidence interval at a fixed error rate. Here we show that, with a small adaptation to the randomized benchmarking procedure, the number of sampled sequences required for a fixed confidence interval is dramatically smaller than could previously be justified. In particular, we show that the number of sampled sequences required is essentially independent of the number of qubits and scales favorably with the average error rate of the system under investigation. We also show that the number of samples required for long sequence lengths can be made substantially smaller than previous rigorous results (even for single qubits) as long as the noise process under investigation is not unitary. Our results bring rigorous randomized benchmarking on systems with many qubits into the realm of experimental feasibility.
@article{1701.04299, author = {Helsen, Jonas and Wallman, Joel J. and Flammia, Steven T. and Wehner, Stephanie}, doi = {10.1103/PhysRevA.100.032304}, archiveprefix = {arXiv}, eprint = {1701.04299}, journal = {Phys. Rev. A}, title = {Multi-qubit Randomized Benchmarking Using Few Samples}, volume = {100}, pages = {032304}, year = {2019} } -
 Limits on the storage of quantum information in a volume of spaceSteven T. Flammia, Jeongwan Haah, Michael J. Kastoryano, and Isaac H. KimQuantum, 1 4 2017.
Limits on the storage of quantum information in a volume of spaceSteven T. Flammia, Jeongwan Haah, Michael J. Kastoryano, and Isaac H. KimQuantum, 1 4 2017.We study the fundamental limits on the reliable storage of quantum information in lattices of qubits by deriving tradeoff bounds for approximate quantum error correcting codes. We introduce a notion of local approximate correctability and code distance, and give a number of equivalent formulations thereof, generalizing various exact error-correction criteria. Our tradeoff bounds relate the number of physical qubits n, the number of encoded qubits k, the code distance d, the accuracy parameter δ that quantifies how well the erasure channel can be reversed, and the locality parameter ℓ that specifies the length scale at which the recovery operation can be done. In a regime where the recovery is successful to accuracy ϵ that is exponentially small in ℓ, which is the case for perturbations of local commuting projector codes, our bound reads k d2/(D−1) ≤ O(n (log n)2D/(D−1)) for codes on D-dimensional lattices of Euclidean metric. We also find that the code distance of any local approximate code cannot exceed O(ℓn(D−1)/D) if δ ≤ O(ℓ n−1/D). As a corollary of our formulation of correctability in terms of logical operator avoidance, we show that the code distance d and the size d̃ of a minimal region that can support all approximate logical operators satisfies d̃ d1/(D−1) ≤ O(n ℓD/(D−1)), where the logical operators are accurate up to O((nδ/d)1/2) in operator norm. Finally, we prove that for two-dimensional systems if logical operators can be approximated by operators supported on constant-width flexible strings, then the dimension of the code space must be bounded. This supports one of the assumptions of algebraic anyon theories, that there exist only finitely many anyon types.
@article{1610.06169, author = {Flammia, Steven T. and Haah, Jeongwan and Kastoryano, Michael J. and Kim, Isaac H.}, doi = {10.22331/q-2017-04-25-4}, archiveprefix = {arXiv}, eprint = {1610.06169}, journal = {Quantum}, title = {Limits on the storage of quantum information in a volume of space}, volume = {1}, pages = {4}, year = {2017} } -
 Explaining quantum correlations through evolution of causal modelsRobin Harper, Robert J. Chapman, Christopher Ferrie, Christopher Granade, Richard Kueng, Daniel Naoumenko, Steven T. Flammia, and Alberto PeruzzoPhys. Rev. A, 95 042120 2017.
Explaining quantum correlations through evolution of causal modelsRobin Harper, Robert J. Chapman, Christopher Ferrie, Christopher Granade, Richard Kueng, Daniel Naoumenko, Steven T. Flammia, and Alberto PeruzzoPhys. Rev. A, 95 042120 2017.We propose a framework for the systematic and quantitative generalization of Bell’s theorem using causal networks. We first consider the multi-objective optimization problem of matching observed data while minimizing the causal effect of nonlocal variables and prove an inequality for the optimal region that both strengthens and generalizes Bell’s theorem. To solve the optimization problem (rather than simply bound it), we develop a novel genetic algorithm treating as individuals causal networks. By applying our algorithm to a photonic Bell experiment, we demonstrate the trade-off between the quantitative relaxation of one or more local causality assumptions and the ability of data to match quantum correlations.
@article{1608.03281, author = {Harper, Robin and Chapman, Robert J. and Ferrie, Christopher and Granade, Christopher and Kueng, Richard and Naoumenko, Daniel and Flammia, Steven T. and Peruzzo, Alberto}, doi = {10.1103/PhysRevA.95.042120}, archiveprefix = {arXiv}, eprint = {1608.03281}, journal = {Phys. Rev. A}, title = {Explaining quantum correlations through evolution of causal models}, volume = {95}, pages = {042120}, year = {2017} } -
 Estimating the fidelity of T gates using standard interleaved randomized benchmarkingRobin Harper, and Steven T. FlammiaQuantum Science and Technology, 2 015008 2017.
Estimating the fidelity of T gates using standard interleaved randomized benchmarkingRobin Harper, and Steven T. FlammiaQuantum Science and Technology, 2 015008 2017.Randomized benchmarking (RB) is an important protocol for robustly characterizing the error rates of quantum gates. The technique is typically applied to the Clifford gates since they form a group that satisfies a convenient technical condition of forming a unitary 2-design, in addition to having a tight connection to fault-tolerant quantum computing and an efficient classical simulation. In order to achieve universal quantum computing one must add at least one additional gate such as the T gate (also known as the π/8 gate). Here we propose and analyze a simple variation of the standard interleaved RB protocol that can accurately estimate the average fidelity of the T gate while retaining the many advantages of a unitary 2-design and the fidelity guarantees that such a design delivers, as well as the efficient classical simulation property of the Clifford group. Our work complements prior methods that have succeeded in estimating T gate fidelities, but only by relaxing the 2-design constraint and using a more complicated data analysis.
@article{1608.02943, author = {Harper, Robin and Flammia, Steven T.}, doi = {10.1088/2058-9565/aa5f8d}, archiveprefix = {arXiv}, eprint = {1608.02943}, journal = {Quantum Science and Technology}, title = {Estimating the fidelity of {T} gates using standard interleaved randomized benchmarking}, volume = {2}, pages = {015008}, year = {2017} } -
 Approximate symmetries of HamiltoniansChristopher T. Chubb, and Steven T. FlammiaJournal of Mathematical Physics, 58 082202 2017.
Approximate symmetries of HamiltoniansChristopher T. Chubb, and Steven T. FlammiaJournal of Mathematical Physics, 58 082202 2017.We explore the relationship between approximate symmetries of a gapped Hamiltonian and the structure of its ground space. We start by showing that approximate symmetry operators—unitary operators whose commutators with the Hamiltonian have norms that are sufficiently small—which possess certain mutual commutation relations can be restricted to the ground space with low distortion. We generalize the Stone-von Neumann theorem to matrices that approximately satisfy the canonical (Heisenberg-Weyl-type) commutation relations, and use this to show that approximate symmetry operators can certify the degeneracy of the ground space even though they only approximately form a group. Importantly, the notions of "approximate" and "small" are all independent of the dimension of the ambient Hilbert space, and depend only on the degeneracy in the ground space. Our analysis additionally holds for any gapped band of sufficiently small width in the excited spectrum of the Hamiltonian, and we discuss applications of these ideas to topological quantum phases of matter and topological quantum error correcting codes. Finally, in our analysis we also provide an exponential improvement upon bounds concerning the existence of shared approximate eigenvectors of approximately commuting operators which may be of independent interest.
@article{1608.02600, author = {Chubb, Christopher T. and Flammia, Steven T.}, doi = {10.1063/1.4998921}, archiveprefix = {arXiv}, eprint = {1608.02600}, journal = {Journal of Mathematical Physics}, title = {Approximate symmetries of {H}amiltonians}, volume = {58}, pages = {082202}, year = {2017} } -
 Experimental quantum compressed sensing for a seven-qubit systemC. A. Riofrı́o, D. Gross, S. T. Flammia, T. Monz, D. Nigg, R. Blatt, and J. EisertNature Comm., 8 15305 2017.
Experimental quantum compressed sensing for a seven-qubit systemC. A. Riofrı́o, D. Gross, S. T. Flammia, T. Monz, D. Nigg, R. Blatt, and J. EisertNature Comm., 8 15305 2017.Well-controlled quantum devices with their increasing system size face a new roadblock hindering further development of quantum technologies: The effort of quantum tomography—the characterization of processes and states within a quantum device—scales unfavorably to the point that state-of-the-art systems can no longer be treated. Quantum compressed sensing mitigates this problem by reconstructing the state from an incomplete set of observables. In this work, we present an experimental implementation of compressed tomography of a seven qubit system—the largest-scale realization to date—and we introduce new numerical methods in order to scale the reconstruction to this dimension. Originally, compressed sensing has been advocated for density matrices with few non-zero eigenvalues. Here, we argue that the low-rank estimates provided by compressed sensing can be appropriate even in the general case. The reason is that statistical noise often allows only for the leading eigenvectors to be reliably reconstructed: We find that the remaining eigenvectors behave in a way consistent with a random matrix model that carries no information about the true state. We report a reconstruction of quantum states from a topological color code of seven qubits, prepared in a trapped ion architecture, based on tomographically incomplete data involving 127 Pauli basis measurement settings only, repeated 100 times each.
@article{1608.02263, author = {Riofr\'{\i}o, C. A. and Gross, D. and Flammia, S. T. and Monz, T. and Nigg, D. and Blatt, R. and Eisert, J.}, doi = {10.1038/ncomms15305}, archiveprefix = {arXiv}, eprint = {1608.02263}, journal = {Nature Comm.}, title = {Experimental quantum compressed sensing for a seven-qubit system}, volume = {8}, pages = {15305}, year = {2017} } -
 Practical adaptive quantum tomographyChristopher Granade, Christopher Ferrie, and Steven T. FlammiaNew J. Phys., 19 113017 2017.
Practical adaptive quantum tomographyChristopher Granade, Christopher Ferrie, and Steven T. FlammiaNew J. Phys., 19 113017 2017.We introduce a fast and accurate heuristic for adaptive tomography that addresses many of the limitations of prior methods. Previous approaches were either too computationally intensive or tailored to handle special cases such as single qubits or pure states. By contrast, our approach combines the efficiency of online optimization with generally applicable and well-motivated data-processing techniques. We numerically demonstrate these advantages in several scenarios including mixed states, higher-dimensional systems, and restricted measurements.
@article{1605.05039, author = {Granade, Christopher and Ferrie, Christopher and Flammia, Steven T.}, doi = {10.1088/1367-2630/aa8fe6}, archiveprefix = {arXiv}, eprint = {1605.05039}, journal = {New J. Phys.}, title = {Practical adaptive quantum tomography}, volume = {19}, pages = {113017}, year = {2017} } -
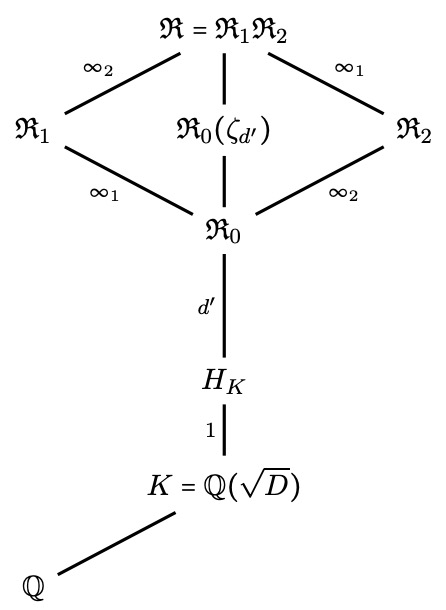 Generating Ray Class Fields of Real Quadratic Fields via Complex Equiangular LinesMarcus Appleby, Steven Flammia, Gary McConnell, and Jon YardActa Arith., 192 211–233 2020.
Generating Ray Class Fields of Real Quadratic Fields via Complex Equiangular LinesMarcus Appleby, Steven Flammia, Gary McConnell, and Jon YardActa Arith., 192 211–233 2020.For certain real quadratic fields K with sufficiently small discriminant we produce explicit unit generators for specific ray class fields of K using a numerical method that arose in the study of complete sets of equiangular lines in ℂd (known in quantum information as symmetric informationally complete measurements or SICs). The construction in low dimensions suggests a general recipe for producing unit generators in infinite towers of ray class fields above arbitrary real quadratic K, and we summarise this in a conjecture. There are indications [19,20] that the logarithms of these canonical units are related to the values of L-functions associated to the extensions, following the programme laid out in the Stark Conjectures.
@article{1604.06098, author = {Appleby, Marcus and Flammia, Steven and McConnell, Gary and Yard, Jon}, doi = {10.4064/aa180508-21-6}, archiveprefix = {arXiv}, eprint = {1604.06098}, journal = {Acta Arith.}, title = {Generating Ray Class Fields of Real Quadratic Fields via Complex Equiangular Lines}, volume = {192}, pages = {211--233}, year = {2020} } -
 Detecting Topological Order with Ribbon OperatorsJacob C. Bridgeman, Steven T. Flammia, and David PoulinPhys. Rev. B, 94 205123 2016.
Detecting Topological Order with Ribbon OperatorsJacob C. Bridgeman, Steven T. Flammia, and David PoulinPhys. Rev. B, 94 205123 2016.We introduce a numerical method for identifying topological order in two-dimensional models based on one-dimensional bulk operators. The idea is to identify approximate symmetries supported on thin strips through the bulk that behave as string operators associated to an anyon model. We can express these ribbon operators in matrix product form and define a cost function that allows us to efficiently optimize over this ansatz class. We test this method on spin models with abelian topological order by finding ribbon operators for ℤd quantum double models with local fields and Ising-like terms. In addition, we identify ribbons in the abelian phase of Kitaev’s honeycomb model which serve as the logical operators of the encoded qubit for the quantum error-correcting code. We further identify the topologically encoded qubit in the quantum compass model, and show that despite this qubit, the model does not support topological order. Finally, we discuss how the method supports generalizations for detecting nonabelian topological order.
@article{1603.02275, author = {Bridgeman, Jacob C. and Flammia, Steven T. and Poulin, David}, doi = {10.1103/PhysRevB.94.205123}, archiveprefix = {arXiv}, eprint = {1603.02275}, journal = {Phys. Rev. B}, title = {Detecting Topological Order with Ribbon Operators}, volume = {94}, pages = {205123}, year = {2016} } -
 Comparing Experiments to the Fault-Tolerance ThresholdRichard Kueng, David M. Long, Andrew C. Doherty, and Steven T. FlammiaPhys. Rev. Lett., 117 170502 2016.
Comparing Experiments to the Fault-Tolerance ThresholdRichard Kueng, David M. Long, Andrew C. Doherty, and Steven T. FlammiaPhys. Rev. Lett., 117 170502 2016.Achieving error rates that meet or exceed the fault-tolerance threshold is a central goal for quantum computing experiments, and measuring these error rates using randomized benchmarking is now routine. However, direct comparison between measured error rates and thresholds is complicated by the fact that benchmarking estimates average error rates while thresholds reflect worst-case behavior when a gate is used as part of a large computation. These two measures of error can differ by orders of magnitude in the regime of interest. Here we facilitate comparison between the experimentally accessible average error rates and the worst-case quantities that arise in current threshold theorems by deriving relations between the two for a variety of physical noise sources. Our results indicate that it is coherent errors that lead to an enormous mismatch between average and worst case, and we quantify how well these errors must be controlled to ensure fair comparison between average error probabilities and fault-tolerance thresholds.
@article{1510.05653, author = {Kueng, Richard and Long, David M. and Doherty, Andrew C. and Flammia, Steven T.}, doi = {10.1103/PhysRevLett.117.170502}, archiveprefix = {arXiv}, eprint = {1510.05653}, journal = {Phys. Rev. Lett.}, title = {Comparing Experiments to the Fault-Tolerance Threshold}, volume = {117}, pages = {170502}, year = {2016} } -
 Symmetry-respecting real-space renormalization for the quantum Ashkin-Teller modelAroon O’Brien, Stephen D. Bartlett, Andrew C. Doherty, and Steven T. FlammiaPhys. Rev. E, 92 042163 2015.
Symmetry-respecting real-space renormalization for the quantum Ashkin-Teller modelAroon O’Brien, Stephen D. Bartlett, Andrew C. Doherty, and Steven T. FlammiaPhys. Rev. E, 92 042163 2015.We use a simple real-space renormalization group approach to investigate the critical behavior of the quantum Ashkin-Teller model, a one-dimensional quantum spin chain possessing a line of criticality along which critical exponents vary continuously. This approach, which is based on exploiting the on-site symmetry of the model, has been shown to be surprisingly accurate for predicting some aspects of the critical behavior of the Ising model. Our investigation explores this approach in more generality, in a model where the critical behavior has a richer structure but which reduces to the simpler Ising case at a special point. We demonstrate that the correlation length critical exponent as predicted from this real-space renormalization group approach is in broad agreement with the corresponding results from conformal field theory along the line of criticality. Near the Ising special point, the error in the estimated critical exponent from this simple method is comparable to that of numerically-intensive simulations based on much more sophisticated methods, although the accuracy decreases away from the decoupled Ising model point.
@article{1507.00038, author = {O'Brien, Aroon and Bartlett, Stephen D. and Doherty, Andrew C. and Flammia, Steven T.}, doi = {10.1103/PhysRevE.92.042163}, archiveprefix = {arXiv}, eprint = {1507.00038}, journal = {Phys. Rev. E}, title = {Symmetry-respecting real-space renormalization for the quantum {A}shkin-{T}eller model}, volume = {92}, pages = {042163}, year = {2015} } -
 Classical Simulation of Quantum Error Correction in a Fibonacci Anyon CodeSimon Burton, Courtney G. Brell, and Steven T. FlammiaPhys. Rev. A, 95 022309 2017.
Classical Simulation of Quantum Error Correction in a Fibonacci Anyon CodeSimon Burton, Courtney G. Brell, and Steven T. FlammiaPhys. Rev. A, 95 022309 2017.Classically simulating the dynamics of anyonic excitations in two-dimensional quantum systems is likely intractable in general because such dynamics are sufficient to implement universal quantum computation. However, processes of interest for the study of quantum error correction in anyon systems are typically drawn from a restricted class that displays significant structure over a wide range of system parameters. We exploit this structure to classically simulate, and thereby demonstrate the success of, an error-correction protocol for a quantum memory based on the universal Fibonacci anyon model. We numerically simulate a phenomenological model of the system and noise processes on lattice sizes of up to 128x128 sites, and find a lower bound on the error-correction threshold of approximately 0.125 errors per edge, which is comparable to those previously known for abelian and (non-universal) nonabelian anyon models.
@article{1506.03815, author = {Burton, Simon and Brell, Courtney G. and Flammia, Steven T.}, doi = {10.1103/PhysRevA.95.022309}, archiveprefix = {arXiv}, eprint = {1506.03815}, journal = {Phys. Rev. A}, title = {Classical Simulation of Quantum Error Correction in a Fibonacci Anyon Code}, volume = {95}, pages = {022309}, year = {2017} } -
 The effect of noise correlations on randomized benchmarkingHarrison Ball, Thomas M. Stace, Steven T. Flammia, and Michael J. BiercukPhys. Rev. A, 93 022303 2016.
The effect of noise correlations on randomized benchmarkingHarrison Ball, Thomas M. Stace, Steven T. Flammia, and Michael J. BiercukPhys. Rev. A, 93 022303 2016.Among the most popular and well studied quantum characterization, verification and validation techniques is randomized benchmarking (RB), an important statistical tool used to characterize the performance of physical logic operations useful in quantum information processing. In this work we provide a detailed mathematical treatment of the effect of temporal noise correlations on the outcomes of RB protocols. We provide a fully analytic framework capturing the accumulation of error in RB expressed in terms of a three-dimensional random walk in "Pauli space." Using this framework we derive the probability density function describing RB outcomes (averaged over noise) for both Markovian and correlated errors, which we show is generally described by a gamma distribution with shape and scale parameters depending on the correlation structure. Long temporal correlations impart large nonvanishing variance and skew in the distribution towards high-fidelity outcomes – consistent with existing experimental data – highlighting potential finite-sampling pitfalls and the divergence of the mean RB outcome from worst-case errors in the presence of noise correlations. We use the Filter-transfer function formalism to reveal the underlying reason for these differences in terms of effective coherent averaging of correlated errors in certain random sequences. We conclude by commenting on the impact of these calculations on the utility of single-metric approaches to quantum characterization, verification, and validation.
@article{1504.05307, author = {Ball, Harrison and Stace, Thomas M. and Flammia, Steven T. and Biercuk, Michael J.}, doi = {10.1103/PhysRevA.93.022303}, archiveprefix = {arXiv}, eprint = {1504.05307}, journal = {Phys. Rev. A}, title = {The effect of noise correlations on randomized benchmarking}, volume = {93}, pages = {022303}, year = {2016} } -
 Error Compensation of Single-Qubit Gates in a Surface Electrode Ion Trap Using Composite PulsesEmily Mount, Chingiz Kabytayev, Stephen Crain, Robin Harper, So-Young Baek, Geert Vrijsen, Steven Flammia, Kenneth R. Brown, Peter Maunz, and Jungsang KimPhys. Rev. A, 92 060301 2015.
Error Compensation of Single-Qubit Gates in a Surface Electrode Ion Trap Using Composite PulsesEmily Mount, Chingiz Kabytayev, Stephen Crain, Robin Harper, So-Young Baek, Geert Vrijsen, Steven Flammia, Kenneth R. Brown, Peter Maunz, and Jungsang KimPhys. Rev. A, 92 060301 2015.The fidelity of laser-driven quantum logic operations on trapped ion qubits tend to be lower than microwave-driven logic operations due to the difficulty of stabilizing the driving fields at the ion location. Through stabilization of the driving optical fields and use of composite pulse sequences, we demonstrate high fidelity single-qubit gates for the hyperfine qubit of a 171Yb+ ion trapped in a microfabricated surface electrode ion trap. Gate error is characterized using a randomized benchmarking protocol, and an average error per randomized Clifford group gate of 3.6(3)×10−4 is measured. We also report experimental realization of palindromic pulse sequences that scale efficiently in sequence length.
@article{1504.01440, author = {Mount, Emily and Kabytayev, Chingiz and Crain, Stephen and Harper, Robin and Baek, So-Young and Vrijsen, Geert and Flammia, Steven and Brown, Kenneth R. and Maunz, Peter and Kim, Jungsang}, doi = {10.1103/PhysRevA.92.060301}, archiveprefix = {arXiv}, eprint = {1504.01440}, journal = {Phys. Rev. A}, title = {Error Compensation of Single-Qubit Gates in a Surface Electrode Ion Trap Using Composite Pulses}, volume = {92}, pages = {060301}, year = {2015} } -
 Estimating the Coherence of NoiseJoel J. Wallman, Christopher Granade, Robin Harper, and Steven T. FlammiaNew J. Phys., 17 113020 2015.
Estimating the Coherence of NoiseJoel J. Wallman, Christopher Granade, Robin Harper, and Steven T. FlammiaNew J. Phys., 17 113020 2015.Noise mechanisms in quantum systems can be broadly characterized as either coherent (i.e., unitary) or incoherent. For a given fixed average error rate, coherent noise mechanisms will generally lead to a larger worst-case error than incoherent noise. We show that the coherence of a noise source can be quantified by the unitarity, which we relate to the average change in purity averaged over input pure states. We then show that the unitarity can be efficiently estimated using a protocol based on randomized benchmarking that is efficient and robust to state-preparation and measurement errors. We also show that the unitarity provides a lower bound on the optimal achievable gate infidelity under a given noisy process.
@article{1503.07865, author = {Wallman, Joel J. and Granade, Christopher and Harper, Robin and Flammia, Steven T.}, doi = {10.1088/1367-2630/17/11/113020}, archiveprefix = {arXiv}, eprint = {1503.07865}, journal = {New J. Phys.}, title = {Estimating the Coherence of Noise}, volume = {17}, pages = {113020}, year = {2015} } -
 Computing the Degenerate Ground Space of Gapped Spin Chains in Polynomial TimeChristopher T. Chubb, and Steven T. FlammiaChicago Journal of Theoretical Computer Science, 2016 9 2016.
Computing the Degenerate Ground Space of Gapped Spin Chains in Polynomial TimeChristopher T. Chubb, and Steven T. FlammiaChicago Journal of Theoretical Computer Science, 2016 9 2016.Given a gapped Hamiltonian of a spin chain, we give a polynomial-time algorithm for finding the degenerate ground space projector. The output is an orthonormal set of matrix product states that approximate the true ground space projector up to an inverse polynomial error in any Schatten norm, with a runtime exponential in the degeneracy. Our algorithm is an extension of the recent algorithm of Landau, Vazirani, and Vidick for the nondegenerate case, and it includes the recent improvements due to Huang. The main new idea is to incorporate the local distinguishability of ground states on the half-chain to ensure that the algorithm returns a complete set of global ground states.
@article{1502.06967, author = {Chubb, Christopher T. and Flammia, Steven T.}, doi = {10.4086/cjtcs.2016.009}, archiveprefix = {arXiv}, eprint = {1502.06967}, journal = {Chicago Journal of Theoretical Computer Science}, title = {Computing the Degenerate Ground Space of Gapped Spin Chains in Polynomial Time}, volume = {2016}, pages = {9}, year = {2016} } -
 Non-exponential Fidelity Decay in Randomized Benchmarking with Low-Frequency NoiseM. A. Fogarty, M. Veldhorst, R. Harper, C. H. Yang, S. D. Bartlett, S. T. Flammia, and A. S. DzurakPhys. Rev. A, 92 022326 2015.
Non-exponential Fidelity Decay in Randomized Benchmarking with Low-Frequency NoiseM. A. Fogarty, M. Veldhorst, R. Harper, C. H. Yang, S. D. Bartlett, S. T. Flammia, and A. S. DzurakPhys. Rev. A, 92 022326 2015.We show that non-exponential fidelity decays in randomized benchmarking experiments on quantum dot qubits are consistent with numerical simulations that incorporate low-frequency noise. By expanding standard randomized benchmarking analysis to this experimental regime, we find that such non-exponential decays are better modeled by multiple exponential decay rates, leading to an instantaneous control fidelity for isotopically-purified-silicon MOS quantum dot qubits which can be as high as 99.9% when low-frequency noise conditions and system calibrations are favorable. These advances in qubit characterization and validation methods underpin the considerable prospects for silicon as a qubit platform for fault-tolerant quantum computation.
@article{1502.05119, author = {Fogarty, M. A. and Veldhorst, M. and Harper, R. and Yang, C. H. and Bartlett, S. D. and Flammia, S. T. and Dzurak, A. S.}, doi = {10.1103/PhysRevA.92.022326}, archiveprefix = {arXiv}, eprint = {1502.05119}, journal = {Phys. Rev. A}, title = {Non-exponential Fidelity Decay in Randomized Benchmarking with Low-Frequency Noise}, volume = {92}, pages = {022326}, year = {2015} } -
 Sparse Quantum Codes from Quantum CircuitsDave Bacon, Steven T. Flammia, Aram W. Harrow, and Jonathan ShiIEEE Transactions on Information Theory, 63 2464–2479 2017.
Sparse Quantum Codes from Quantum CircuitsDave Bacon, Steven T. Flammia, Aram W. Harrow, and Jonathan ShiIEEE Transactions on Information Theory, 63 2464–2479 2017.We describe a general method for turning quantum circuits into sparse quantum subsystem codes. The idea is to turn each circuit element into a set of low-weight gauge generators that enforce the input-output relations of that circuit element. Using this prescription, we can map an arbitrary stabilizer code into a new subsystem code with the same distance and number of encoded qubits but where all the generators have constant weight, at the cost of adding some ancilla qubits. With an additional overhead of ancilla qubits, the new code can also be made spatially local. Applying our construction to certain concatenated stabilizer codes yields families of subsystem codes with constant-weight generators and with minimum distance d=n1−ϵ, where ϵ=O(1/√log n). For spatially local codes in D dimensions we nearly saturate a bound due to Bravyi and Terhal and achieve d=n1−ϵ−1/D. Previously the best code distance achievable with constant-weight generators in any dimension, due to Freedman, Meyer and Luo, was O(√(n log n)) for a stabilizer code.
@article{1411.3334, author = {Bacon, Dave and Flammia, Steven T. and Harrow, Aram W. and Shi, Jonathan}, doi = {10.1109/TIT.2017.2663199}, archiveprefix = {arXiv}, eprint = {1411.3334}, journal = {IEEE Transactions on Information Theory}, number = {4}, pages = {2464--2479}, title = {Sparse Quantum Codes from Quantum Circuits}, volume = {63}, year = {2017} } -
 Adiabatic topological quantum computingChris Cesare, Andrew J. Landahl, Dave Bacon, Steven T. Flammia, and Alice NeelsPhys. Rev. A, 92 012336 2015.
Adiabatic topological quantum computingChris Cesare, Andrew J. Landahl, Dave Bacon, Steven T. Flammia, and Alice NeelsPhys. Rev. A, 92 012336 2015.Topological quantum computing promises error-resistant quantum computation without active error correction. However, there is a worry that during the process of executing quantum gates by braiding anyons around each other, extra anyonic excitations will be created that will disorder the encoded quantum information. Here we explore this question in detail by studying adiabatic code deformations on Hamiltonians based on topological codes, notably Kitaev’s surface codes and the more recently discovered color codes. We develop protocols that enable universal quantum computing by adiabatic evolution in a way that keeps the energy gap of the system constant with respect to the computation size and introduces only simple local Hamiltonian interactions. This allows one to perform holonomic quantum computing with these topological quantum computing systems. The tools we develop allow one to go beyond numerical simulations and understand these processes analytically.
@article{1406.2690, author = {Cesare, Chris and Landahl, Andrew J. and Bacon, Dave and Flammia, Steven T. and Neels, Alice}, doi = {10.1103/PhysRevA.92.012336}, archiveprefix = {arXiv}, eprint = {1406.2690}, journal = {Phys. Rev. A}, title = {Adiabatic topological quantum computing}, volume = {92}, pages = {012336}, year = {2015} } -
 Randomized Benchmarking with ConfidenceJoel J. Wallman, and Steven T. FlammiaNew J. Phys., 16 103032 2014.
Randomized Benchmarking with ConfidenceJoel J. Wallman, and Steven T. FlammiaNew J. Phys., 16 103032 2014.Randomized benchmarking is a promising tool for characterizing the noise in experimental implementations of quantum systems. In this paper, we prove that the estimates produced by randomized benchmarking (both standard and interleaved) for arbitrary Markovian noise sources are remarkably precise by showing that the variance due to sampling random gate sequences is small. We discuss how to choose experimental parameters, in particular the number and lengths of random sequences, in order to characterize average gate errors with rigorous confidence bounds. We also show that randomized benchmarking can be used to reliably characterize time-dependent Markovian noise (e.g., when noise is due to a magnetic field with fluctuating strength). Moreover, we identify a necessary property for time-dependent noise that is violated by some sources of non-Markovian noise, which provides a test for non-Markovianity.
@article{1404.6025, author = {Wallman, Joel J. and Flammia, Steven T.}, doi = {10.1088/1367-2630/16/10/103032}, archiveprefix = {arXiv}, eprint = {1404.6025}, journal = {New J. Phys.}, title = {Randomized Benchmarking with Confidence}, volume = {16}, pages = {103032}, year = {2014} } -
 Local PT symmetry violates the no-signaling principleYi-Chan Lee, Min-Hsiu Hsieh, Steven T. Flammia, and Ray-Kuang LeePhys. Rev. Lett., 112 130404 2014.
Local PT symmetry violates the no-signaling principleYi-Chan Lee, Min-Hsiu Hsieh, Steven T. Flammia, and Ray-Kuang LeePhys. Rev. Lett., 112 130404 2014.Bender et al. have developed PT-symmetric quantum theory as an extension of quantum theory to non-Hermitian Hamiltonians. We show that when this model has a local PT symmetry acting on composite systems it violates the non-signaling principle of relativity. Since the case of global PT symmetry is known to reduce to standard quantum mechanics, this shows that the PT-symmetric theory is either a trivial extension or likely false as a fundamental theory.
@article{1312.3395, author = {Lee, Yi-Chan and Hsieh, Min-Hsiu and Flammia, Steven T. and Lee, Ray-Kuang}, doi = {10.1103/PhysRevLett.112.130404}, archiveprefix = {arXiv}, eprint = {1312.3395}, journal = {Phys. Rev. Lett.}, title = {Local {PT} symmetry violates the no-signaling principle}, volume = {112}, pages = {130404}, year = {2014} } -
 Thermalization, Error-Correction, and Memory Lifetime for Ising Anyon SystemsCourtney G. Brell, Simon Burton, Guillaume Dauphinais, Steven T. Flammia, and David PoulinPhys. Rev. X, 4 031058 2014.
Thermalization, Error-Correction, and Memory Lifetime for Ising Anyon SystemsCourtney G. Brell, Simon Burton, Guillaume Dauphinais, Steven T. Flammia, and David PoulinPhys. Rev. X, 4 031058 2014.We consider two-dimensional lattice models that support Ising anyonic excitations and are coupled to a thermal bath. We propose a phenomenological model for the resulting short-time dynamics that includes pair-creation, hopping, braiding, and fusion of anyons. By explicitly constructing topological quantum error-correcting codes for this class of system, we use our thermalization model to estimate the lifetime of the quantum information stored in the encoded spaces. To decode and correct errors in these codes, we adapt several existing topological decoders to the non-Abelian setting. We perform large-scale numerical simulations of these two-dimensional Ising anyon systems and find that the thresholds of these models range between 13% to 25%. To our knowledge, these are the first numerical threshold estimates for quantum codes without explicit additive structure.
@article{1311.0019, author = {Brell, Courtney G. and Burton, Simon and Dauphinais, Guillaume and Flammia, Steven T. and Poulin, David}, doi = {10.1103/PhysRevX.4.031058}, archiveprefix = {arXiv}, eprint = {1311.0019}, journal = {Phys. Rev. X}, title = {Thermalization, Error-Correction, and Memory Lifetime for {I}sing Anyon Systems}, volume = {4}, pages = {031058}, year = {2014} } -
 Programmable quantum simulation by dynamic Hamiltonian engineeringDavid L. Hayes, Steven T. Flammia, and Michael J. BiercukNew J. Phys., 16 083027 2014.
Programmable quantum simulation by dynamic Hamiltonian engineeringDavid L. Hayes, Steven T. Flammia, and Michael J. BiercukNew J. Phys., 16 083027 2014.Quantum simulation is a promising near term application for mesoscale quantum information processors, with the potential to solve computationally intractable problems at the scale of just a few dozen interacting quantum systems. Recent experiments in a range of technical platforms have demonstrated the basic functionality of quantum simulation applied to quantum magnetism, quantum phase transitions, and relativistic quantum mechanics. In all cases, the underlying hardware platforms restrict the achievable inter-particle interaction, forming a serious constraint on the ability to realize a versatile, programmable quantum simulator. In this work, we address this problem by developing novel sequences of unitary operations that engineer desired effective Hamiltonians in the time-domain. The result is a hybrid programmable analog simulator permitting a broad class of interacting spin-lattice models to be generated starting only with an arbitrary long-range native inter-particle interaction and single-qubit addressing. Specifically, our approach permits the generation of all symmetrically coupled translation-invariant two-body Hamiltonians with homogeneous on-site terms, a class which includes all spin-1/2 XYZ chains, but generalized to include long-range couplings. Building on previous work proving that universal simulation is possible using both entangling gates and single-qubit unitaries, we show that determining the "program" of unitary pulses to implement an arbitrary spin Hamiltonian can be formulated as a linear program that runs in polynomial time and scales efficiently in hardware resources. Our analysis extends from circuit model quantum information to adiabatic quantum evolutions, where our approach allows for the creation of non-native ground state solutions to a computation.
@article{1309.6736, author = {Hayes, David L. and Flammia, Steven T. and Biercuk, Michael J.}, doi = {10.1088/1367-2630/16/8/083027}, archiveprefix = {arXiv}, eprint = {1309.6736}, journal = {New J. Phys.}, title = {Programmable quantum simulation by dynamic {H}amiltonian engineering}, volume = {16}, pages = {083027}, year = {2014} } -
 Adiabatic Quantum TransistorsDave Bacon, Steven T. Flammia, and Gregory M. CrosswhitePhys. Rev. X, 3 021015 2013.
Adiabatic Quantum TransistorsDave Bacon, Steven T. Flammia, and Gregory M. CrosswhitePhys. Rev. X, 3 021015 2013.We describe a many-body quantum system which can be made to quantum compute by the adiabatic application of a large applied field to the system. Prior to the application of the field quantum information is localized on one boundary of the device, and after the application of the field this information has propagated to the other side of the device with a quantum circuit applied to the information. The applied circuit depends on the many-body Hamiltonian of the material, and the computation takes place in a degenerate ground space with symmetry-protected topological order. Such adiabatic quantum transistors are universal adiabatic quantum computing devices which have the added benefit of being modular. Here we describe this model, provide arguments for why it is an efficient model of quantum computing, and examine these many-body systems in the presence of a noisy environment.
@article{1207.2769, author = {Bacon, Dave and Flammia, Steven T. and Crosswhite, Gregory M.}, doi = {10.1103/PhysRevX.3.021015}, archiveprefix = {arXiv}, eprint = {1207.2769}, journal = {Phys. Rev. X}, title = {Adiabatic Quantum Transistors}, volume = {3}, pages = {021015}, year = {2013} } -
 Quantum Tomography via Compressed Sensing: Error Bounds, Sample Complexity, and Efficient EstimatorsSteven T. Flammia, David Gross, Yi-Kai Liu, and Jens EisertNew J. Phys., 14 095022 2012.
Quantum Tomography via Compressed Sensing: Error Bounds, Sample Complexity, and Efficient EstimatorsSteven T. Flammia, David Gross, Yi-Kai Liu, and Jens EisertNew J. Phys., 14 095022 2012.Intuitively, if a density operator has small rank, then it should be easier to estimate from experimental data, since in this case only a few eigenvectors need to be learned. We prove two complementary results that confirm this intuition. First, we show that a low-rank density matrix can be estimated using fewer copies of the state, i.e., the sample complexity of tomography decreases with the rank. Second, we show that unknown low-rank states can be reconstructed from an incomplete set of measurements, using techniques from compressed sensing and matrix completion. These techniques use simple Pauli measurements, and their output can be certified without making any assumptions about the unknown state. We give a new theoretical analysis of compressed tomography, based on the restricted isometry property (RIP) for low-rank matrices. Using these tools, we obtain near-optimal error bounds, for the realistic situation where the data contains noise due to finite statistics, and the density matrix is full-rank with decaying eigenvalues. We also obtain upper-bounds on the sample complexity of compressed tomography, and almost-matching lower bounds on the sample complexity of any procedure using adaptive sequences of Pauli measurements. Using numerical simulations, we compare the performance of two compressed sensing estimators with standard maximum-likelihood estimation (MLE). We find that, given comparable experimental resources, the compressed sensing estimators consistently produce higher-fidelity state reconstructions than MLE. In addition, the use of an incomplete set of measurements leads to faster classical processing with no loss of accuracy. Finally, we show how to certify the accuracy of a low rank estimate using direct fidelity estimation and we describe a method for compressed quantum process tomography that works for processes with small Kraus rank.
@article{1205.2300, author = {Flammia, Steven T. and Gross, David and Liu, Yi-Kai and Eisert, Jens}, doi = {10.1088/1367-2630/14/9/095022}, archiveprefix = {arXiv}, eprint = {1205.2300}, journal = {New J. Phys.}, title = {Quantum Tomography via Compressed Sensing: Error Bounds, Sample Complexity, and Efficient Estimators}, volume = {14}, pages = {095022}, year = {2012} } -
 Counterexamples to Kalai’s Conjecture CSteven T. Flammia, and Aram W. HarrowQuant. Info. & Comp., 13 1–8 2013.
Counterexamples to Kalai’s Conjecture CSteven T. Flammia, and Aram W. HarrowQuant. Info. & Comp., 13 1–8 2013.We provide two simple counterexamples to Kalai’s Conjecture C and discuss our perspective on the implications for the prospect of large-scale fault-tolerant quantum computation.
@article{1204.3404, author = {Flammia, Steven T. and Harrow, Aram W.}, doi = {10.26421/QIC13.1-2.0001}, archiveprefix = {arXiv}, eprint = {1204.3404}, journal = {Quant. Info. \& Comp.}, title = {Counterexamples to {K}alai's Conjecture {C}}, volume = {13}, pages = {1--8}, year = {2013} } -
 Direct Fidelity Estimation from Few Pauli MeasurementsSteven T. Flammia, and Yi-Kai LiuPhys. Rev. Lett., 106 230501 2011.
Direct Fidelity Estimation from Few Pauli MeasurementsSteven T. Flammia, and Yi-Kai LiuPhys. Rev. Lett., 106 230501 2011.We describe a simple method for certifying that an experimental device prepares a desired quantum state rho. Our method is applicable to any pure state rho, and it provides an estimate of the fidelity between rho and the actual (arbitrary) state in the lab, up to a constant additive error. The method requires measuring only a constant number of Pauli expectation values, selected at random according to an importance-weighting rule. Our method is faster than full tomography by a factor of d, the dimension of the state space, and extends easily and naturally to quantum channels.
@article{1104.4695, author = {Flammia, Steven T. and Liu, Yi-Kai}, doi = {10.1103/PhysRevLett.106.230501}, archiveprefix = {arXiv}, eprint = {1104.4695}, journal = {Phys. Rev. Lett.}, title = {Direct Fidelity Estimation from Few {P}auli Measurements}, volume = {106}, pages = {230501}, year = {2011} } -
 Efficient quantum state tomographyMarcus Cramer, Martin B. Plenio, Steven T. Flammia, David Gross, Stephen D. Bartlett, Rolando Somma, Olivier Landon-Cardinal, Yi-Kai Liu, and David PoulinNat. Commun., 1 149 2010.
Efficient quantum state tomographyMarcus Cramer, Martin B. Plenio, Steven T. Flammia, David Gross, Stephen D. Bartlett, Rolando Somma, Olivier Landon-Cardinal, Yi-Kai Liu, and David PoulinNat. Commun., 1 149 2010.Quantum state tomography, the ability to deduce the state of a quantum system from measured data, is the gold standard for verification and benchmarking of quantum devices. It has been realized in systems with few components, but for larger systems it becomes infeasible because the number of quantum measurements and the amount of computation required to process them grows exponentially in the system size. Here we show that we can do exponentially better than direct state tomography for a wide range of quantum states, in particular those that are well approximated by a matrix product state ansatz. We present two schemes for tomography in 1-D quantum systems and touch on generalizations. One scheme requires unitary operations on a constant number of subsystems, while the other requires only local measurements together with more elaborate post-processing. Both schemes rely only on a linear number of experimental operations and classical postprocessing that is polynomial in the system size. A further strength of the methods is that the accuracy of the reconstructed states can be rigorously certified without any a priori assumptions.
@article{1101.4366, author = {Cramer, Marcus and Plenio, Martin B. and Flammia, Steven T. and Gross, David and Bartlett, Stephen D. and Somma, Rolando and Landon-Cardinal, Olivier and Liu, Yi-Kai and Poulin, David}, doi = {10.1038/ncomms1147}, archiveprefix = {arXiv}, eprint = {1101.4366}, journal = {Nat. Commun.}, title = {Efficient quantum state tomography}, volume = {1}, pages = {149}, year = {2010} } -
 Toric codes and quantum doubles from two-body HamiltoniansCourtney G. Brell, Steven T. Flammia, Stephen D. Bartlett, and Andrew C. DohertyNew J. Phys., 13 053039 2011.
Toric codes and quantum doubles from two-body HamiltoniansCourtney G. Brell, Steven T. Flammia, Stephen D. Bartlett, and Andrew C. DohertyNew J. Phys., 13 053039 2011.We present a procedure to obtain the Hamiltonians of the toric code and Kitaev quantum double models as the low-energy limits of entirely two-body Hamiltonians. Our construction makes use of a new type of perturbation gadget based on error-detecting subsystem codes. The procedure is motivated by a PEPS description of the target models, and reproduces the target models’ behavior using only couplings which are natural in terms of the original Hamiltonians. This allows our construction to exactly capture the symmetries of the target models.
@article{1011.1942, author = {Brell, Courtney G. and Flammia, Steven T. and Bartlett, Stephen D. and Doherty, Andrew C.}, doi = {10.1088/1367-2630/13/5/053039}, archiveprefix = {arXiv}, eprint = {1011.1942}, journal = {New J. Phys.}, title = {Toric codes and quantum doubles from two-body {H}amiltonians}, volume = {13}, pages = {053039}, year = {2011} } -
 Computational Difficulty of Computing the Density of StatesBrielin Brown, Steven T. Flammia, and Norbert SchuchPhys. Rev. Lett., 107 040501 2011.
Computational Difficulty of Computing the Density of StatesBrielin Brown, Steven T. Flammia, and Norbert SchuchPhys. Rev. Lett., 107 040501 2011.We study the computational difficulty of computing the ground state degeneracy and the density of states for local Hamiltonians. We show that the difficulty of both problems is exactly captured by a class which we call #BQP, which is the counting version of the quantum complexity class QMA. We show that #BQP is not harder than its classical counting counterpart #P, which in turn implies that computing the ground state degeneracy or the density of states for classical Hamiltonians is just as hard as it is for quantum Hamiltonians.
@article{1010.3060, author = {Brown, Brielin and Flammia, Steven T. and Schuch, Norbert}, doi = {10.1103/PhysRevLett.107.040501}, archiveprefix = {arXiv}, eprint = {1010.3060}, journal = {Phys. Rev. Lett.}, title = {Computational Difficulty of Computing the Density of States}, volume = {107}, pages = {040501}, year = {2011} } -
 Graphical calculus for Gaussian pure statesNicolas C. Menicucci, Steven T. Flammia, and Peter LoockPhys. Rev. A, 83 042335 2011.
Graphical calculus for Gaussian pure statesNicolas C. Menicucci, Steven T. Flammia, and Peter LoockPhys. Rev. A, 83 042335 2011.We provide a unified graphical calculus for all Gaussian pure states, including graph transformation rules for all local and semi-local Gaussian unitary operations, as well as local quadrature measurements. We then use this graphical calculus to analyze continuous-variable (CV) cluster states, the essential resource for one-way quantum computing with CV systems. Current graphical approaches to CV cluster states are only valid in the unphysical limit of infinite squeezing, and the associated graph transformation rules only apply when the initial and final states are of this form. Our formalism applies to all Gaussian pure states and subsumes these rules in a natural way. In addition, the term "CV graph state" currently has several inequivalent definitions in use. Using this formalism we provide a single unifying definition that encompasses all of them. We provide many examples of how the formalism may be used in the context of CV cluster states: defining the "closest" CV cluster state to a given Gaussian pure state and quantifying the error in the approximation due to finite squeezing; analyzing the optimality of certain methods of generating CV cluster states; drawing connections between this new graphical formalism and bosonic Hamiltonians with Gaussian ground states, including those useful for CV one-way quantum computing; and deriving a graphical measure of bipartite entanglement for certain classes of CV cluster states. We mention other possible applications of this formalism and conclude with a brief note on fault tolerance in CV one-way quantum computing.
@article{1007.0725, author = {Menicucci, Nicolas C. and Flammia, Steven T. and van Loock, Peter}, doi = {10.1103/PhysRevA.83.042335}, archiveprefix = {arXiv}, eprint = {1007.0725}, journal = {Phys. Rev. A}, title = {Graphical calculus for {G}aussian pure states}, volume = {83}, pages = {042335}, year = {2011} } -
 The Lie Algebraic Significance of Symmetric Informationally Complete MeasurementsD. M. Appleby, Steven T. Flammia, and Christopher A. FuchsJ. Math. Phys., 52 022202 2011.
The Lie Algebraic Significance of Symmetric Informationally Complete MeasurementsD. M. Appleby, Steven T. Flammia, and Christopher A. FuchsJ. Math. Phys., 52 022202 2011.Examples of symmetric informationally complete positive operator valued measures (SIC-POVMs) have been constructed in every dimension less than or equal to 67. However, it remains an open question whether they exist in all finite dimensions. A SIC-POVM is usually thought of as a highly symmetric structure in quantum state space. However, its elements can equally well be regarded as a basis for the Lie algebra gl(d,C). In this paper we examine the resulting structure constants, which are calculated from the traces of the triple products of the SIC-POVM elements and which, it turns out, characterize the SIC-POVM up to unitary equivalence. We show that the structure constants have numerous remarkable properties. In particular we show that the existence of a SIC-POVM in dimension d is equivalent to the existence of a certain structure in the adjoint representation of gl(d,C). We hope that transforming the problem in this way, from a question about quantum state space to a question about Lie algebras, may help to make the existence problem tractable.
@article{1001.0004, author = {Appleby, D. M. and Flammia, Steven T. and Fuchs, Christopher A.}, doi = {10.1063/1.3555805}, archiveprefix = {arXiv}, eprint = {1001.0004}, journal = {J. Math. Phys.}, title = {The {L}ie Algebraic Significance of Symmetric Informationally Complete Measurements}, volume = {52}, pages = {022202}, year = {2011} } -
 Random unitary maps for quantum state reconstructionSeth T. Merkel, Carlos A. Riofrı́o, Steven T. Flammia, and Ivan H. DeutschPhys. Rev. A, 81 032126 2010.
Random unitary maps for quantum state reconstructionSeth T. Merkel, Carlos A. Riofrı́o, Steven T. Flammia, and Ivan H. DeutschPhys. Rev. A, 81 032126 2010.We study the possibility of performing quantum state reconstruction from a measurement record that is obtained as a sequence of expectation values of a Hermitian operator evolving under repeated application of a single random unitary map, U0. We show that while this single-parameter orbit in operator space is not informationally complete, it can be used to yield surprisingly high-fidelity reconstruction. For a d-dimensional Hilbert space with the initial observable in su(d), the measurement record lacks information about a matrix subspace of dimension > d-2 out of the total dimension d2-1. We determine the conditions on U0 such that the bound is saturated, and show they are achieved by almost all pseudorandom unitary matrices. When we further impose the constraint that the physical density matrix must be positive, we obtain even higher fidelity than that predicted from the missing subspace. With prior knowledge that the state is pure, the reconstruction will be perfect (in the limit of vanishing noise) and for arbitrary mixed states, the fidelity is over 0.96, even for small d, and reaching F > 0.99 for d > 9. We also study the implementation of this protocol based on the relationship between random matrices and quantum chaos. We show that the Floquet operator of the quantum kicked top provides a means of generating the required type of measurement record, with implications on the relationship between quantum chaos and information gain.
@article{0912.2101, author = {Merkel, Seth T. and Riofr\'{\i}o, Carlos A. and Flammia, Steven T. and Deutsch, Ivan H.}, doi = {10.1103/PhysRevA.81.032126}, archiveprefix = {arXiv}, eprint = {0912.2101}, journal = {Phys. Rev. A}, title = {Random unitary maps for quantum state reconstruction}, volume = {81}, pages = {032126}, year = {2010} } -
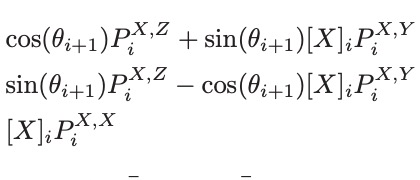 Adiabatic Cluster State Quantum ComputingDave Bacon, and Steven T. FlammiaPhys. Rev. A, 82 030303(R) 2010.
Adiabatic Cluster State Quantum ComputingDave Bacon, and Steven T. FlammiaPhys. Rev. A, 82 030303(R) 2010.Models of quantum computation are important because they change the physical requirements for achieving universal quantum computation (QC). For example, one-way QC requires the preparation of an entangled "cluster" state followed by adaptive measurement on this state, a set of requirements which is different from the standard quantum circuit model. Here we introduce a model based on one-way QC but without measurements (except for the final readout), instead using adiabatic deformation of a Hamiltonian whose initial ground state is the cluster state. This opens the possibility to use the copious results from one-way QC to build more feasible adiabatic schemes.
@article{0912.2098, author = {Bacon, Dave and Flammia, Steven T.}, doi = {10.1103/PhysRevA.82.030303}, archiveprefix = {arXiv}, eprint = {0912.2098}, journal = {Phys. Rev. A}, title = {Adiabatic Cluster State Quantum Computing}, volume = {82}, pages = {030303(R)}, year = {2010} } -
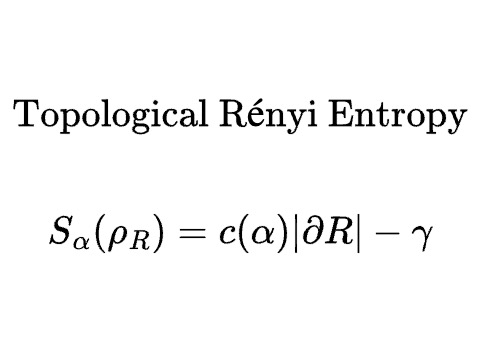 Topological Entanglement Rényi Entropy and Reduced Density Matrix StructureSteven T. Flammia, Alioscia Hamma, Taylor L. Hughes, and Xiao-Gang WenPhys. Rev. Lett., 103 261601 2009.
Topological Entanglement Rényi Entropy and Reduced Density Matrix StructureSteven T. Flammia, Alioscia Hamma, Taylor L. Hughes, and Xiao-Gang WenPhys. Rev. Lett., 103 261601 2009.We generalize the topological entanglement entropy to a family of topological Rényi entropies parametrized by a parameter α, in an attempt to find new invariants for distinguishing topologically ordered phases. We show that, surprisingly, all topological Rényi entropies are the same, independent of α for all non-chiral topological phases. This independence shows that topologically ordered ground-state wavefunctions have reduced density matrices with a certain simple structure, and no additional universal information can be extracted from the entanglement spectrum.
@article{0909.3305, author = {Flammia, Steven T. and Hamma, Alioscia and Hughes, Taylor L. and Wen, Xiao-Gang}, doi = {10.1103/PhysRevLett.103.261601}, archiveprefix = {arXiv}, eprint = {0909.3305}, journal = {Phys. Rev. Lett.}, title = {Topological Entanglement {R}\'{e}nyi Entropy and Reduced Density Matrix Structure}, volume = {103}, pages = {261601}, year = {2009} } -
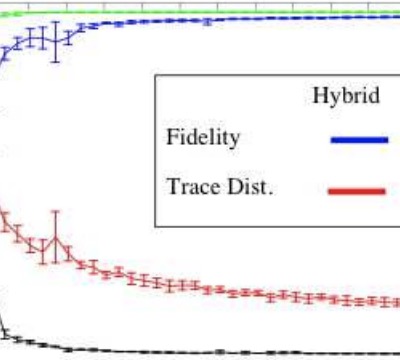 Quantum state tomography via compressed sensingDavid Gross, Yi-Kai Liu, Steven T. Flammia, Stephen Becker, and Jens EisertPhys. Rev. Lett., 105, 150401 (2010) 261601 2009.
Quantum state tomography via compressed sensingDavid Gross, Yi-Kai Liu, Steven T. Flammia, Stephen Becker, and Jens EisertPhys. Rev. Lett., 105, 150401 (2010) 261601 2009.We establish methods for quantum state tomography based on compressed sensing. These methods are specialized for quantum states that are fairly pure, and they offer a significant performance improvement on large quantum systems. In particular, they are able to reconstruct an unknown density matrix of dimension d and rank r using O(r d log2 d) measurement settings, compared to standard methods that require d2 settings. Our methods have several features that make them amenable to experimental implementation: they require only simple Pauli measurements, use fast convex optimization, are stable against noise, and can be applied to states that are only approximately low-rank. The acquired data can be used to certify that the state is indeed close to pure, so no a priori assumptions are needed. We present both theoretical bounds and numerical simulations.
@article{0909.3304, author = {Gross, David and Liu, Yi-Kai and Flammia, Steven T. and Becker, Stephen and Eisert, Jens}, doi = {10.1103/PhysRevLett.105.150401}, archiveprefix = {arXiv}, eprint = {0909.3304}, journal = {Phys. Rev. Lett.}, title = {Quantum state tomography via compressed sensing}, volume = {105, 150401 (2010)}, year = {2009} } -
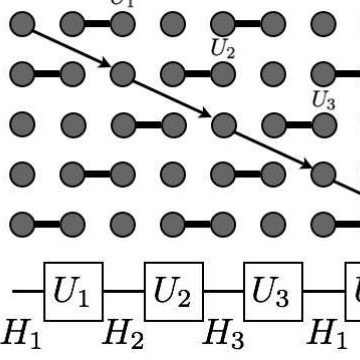 Adiabatic Gate TeleportationDave Bacon, and Steven T. FlammiaPhys. Rev. Lett., 103 120504 2009.
Adiabatic Gate TeleportationDave Bacon, and Steven T. FlammiaPhys. Rev. Lett., 103 120504 2009.The difficulty in producing precisely timed and controlled quantum gates is a significant source of error in many physical implementations of quantum computers. Here we introduce a simple universal primitive, adiabatic gate teleportation, which is robust to timing errors and many control errors and maintains a constant energy gap throughout the computation above a degenerate ground state space. Notably this construction allows for geometric robustness based upon the control of two independent qubit interactions. Further, our piecewise adiabatic evolution easily relates to the quantum circuit model, enabling the use of standard methods from fault-tolerance theory for establishing thresholds.
@article{0905.0901, author = {Bacon, Dave and Flammia, Steven T.}, doi = {10.1103/PhysRevLett.103.120504}, archiveprefix = {arXiv}, eprint = {0905.0901}, journal = {Phys. Rev. Lett.}, title = {Adiabatic Gate Teleportation}, volume = {103}, pages = {120504}, year = {2009} } -
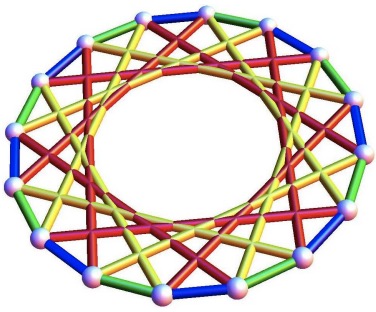 The Optical Frequency Comb as a One-Way Quantum ComputerSteven T. Flammia, Nicolas C. Menicucci, and Oliver PfisterJ. Phys. B, 42 114009 2008.
The Optical Frequency Comb as a One-Way Quantum ComputerSteven T. Flammia, Nicolas C. Menicucci, and Oliver PfisterJ. Phys. B, 42 114009 2008.In the one-way model of quantum computing, quantum algorithms are implemented using only measurements on an entangled initial state. Much of the hard work is done up-front when creating this universal resource, known as a cluster state, on which the measurements are made. Here we detail a new proposal for a scalable method of creating cluster states using only a single multimode optical parametric oscillator (OPO). The method generates a continuous-variable cluster state that is universal for quantum computation and encoded in the quadratures of the optical frequency comb of the OPO. This work expands on the presentation in Phys. Rev. Lett. 101, 130501 (2008).
@article{0811.2799, author = {Flammia, Steven T. and Menicucci, Nicolas C. and Pfister, Oliver}, doi = {10.1088/0953-4075/42/11/114009}, archiveprefix = {arXiv}, eprint = {0811.2799}, journal = {J. Phys. B}, title = {The Optical Frequency Comb as a One-Way Quantum Computer}, volume = {42}, pages = {114009}, year = {2008} } -
 Most quantum states are too entangled to be useful as computational resourcesD. Gross, S. Flammia, and J. EisertPhys. Rev. Lett., 102 190501 2008.
Most quantum states are too entangled to be useful as computational resourcesD. Gross, S. Flammia, and J. EisertPhys. Rev. Lett., 102 190501 2008.It is often argued that entanglement is at the root of the speedup for quantum compared to classical computation, and that one needs a sufficient amount of entanglement for this speedup to be manifest. In measurement-based quantum computing (MBQC), the need for a highly entangled initial state is particularly obvious. Defying this intuition, we show that quantum states can be too entangled to be useful for the purpose of computation. We prove that this phenomenon occurs for a dramatic majority of all states: the fraction of useful n-qubit pure states is less than exp(-n2). Computational universality is hence a rare property in quantum states. This work highlights a new aspect of the question concerning the role entanglement plays for quantum computational speed-ups. The statements remain true if one allows for certain forms of post-selection and also cover the notion of CQ-universality. We identify scale-invariant states resulting from a MERA construction as likely candidates for physically relevant states subject to this effect.
@article{0810.4331, author = {Gross, D. and Flammia, S. and Eisert, J.}, doi = {10.1103/PhysRevLett.102.190501}, archiveprefix = {arXiv}, eprint = {0810.4331}, journal = {Phys. Rev. Lett.}, title = {Most quantum states are too entangled to be useful as computational resources}, volume = {102}, pages = {190501}, year = {2008} } -
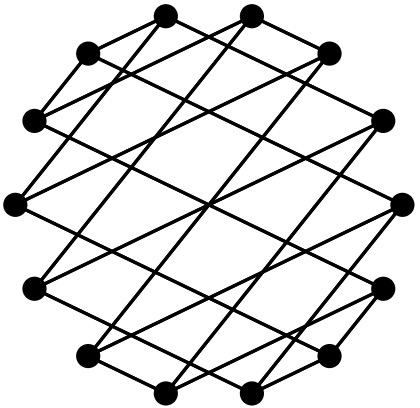 Weighing matrices and optical quantum computingSteven T. Flammia, and Simone SeveriniJ. Phys. A: Math. Theor., 42 065302 2008.
Weighing matrices and optical quantum computingSteven T. Flammia, and Simone SeveriniJ. Phys. A: Math. Theor., 42 065302 2008.Quantum computation in the one-way model requires the preparation of certain resource states known as cluster states. We describe how the construction of continuous-variable cluster states for optical quantum computing relate to the existence of certain families of matrices. The relevant matrices are known as weighing matrices, with a few additional constraints. We prove some results regarding the structure of these matrices, and their associated graphs.
@article{0808.2057, author = {Flammia, Steven T. and Severini, Simone}, doi = {10.1088/1751-8113/42/6/065302}, archiveprefix = {arXiv}, eprint = {0808.2057}, journal = {J. Phys. A: Math. Theor.}, title = {Weighing matrices and optical quantum computing}, volume = {42}, pages = {065302}, year = {2008} } -
 Quantum Metrology: Dynamics vs. EntanglementSergio Boixo, Animesh Datta, Matthew J. Davis, Steven T. Flammia, Anil Shaji, and Carlton M. CavesPhys. Rev. Lett., 101 040403 2008.
Quantum Metrology: Dynamics vs. EntanglementSergio Boixo, Animesh Datta, Matthew J. Davis, Steven T. Flammia, Anil Shaji, and Carlton M. CavesPhys. Rev. Lett., 101 040403 2008.A parameter whose coupling to a quantum probe of n constituents includes all two-body interactions between the constituents can be measured with an uncertainty that scales as 1/n3/2, even when the constituents are initially unentangled. We devise a protocol that achieves the 1/n3/2 scaling without generating any entanglement among the constituents, and we suggest that the protocol might be implemented in a two-component Bose-Einstein condensate.
@article{0805.2180, author = {Boixo, Sergio and Datta, Animesh and Davis, Matthew J. and Flammia, Steven T. and Shaji, Anil and Caves, Carlton M.}, doi = {10.1103/PhysRevLett.101.040403}, archiveprefix = {arXiv}, eprint = {0805.2180}, journal = {Phys. Rev. Lett.}, title = {Quantum Metrology: Dynamics vs. Entanglement}, volume = {101}, pages = {040403}, year = {2008} } -
 One-Way Quantum Computing in the Optical Frequency CombNicolas C. Menicucci, Steven T. Flammia, and Olivier PfisterPhys. Rev. Lett., 101 130501 2008.
One-Way Quantum Computing in the Optical Frequency CombNicolas C. Menicucci, Steven T. Flammia, and Olivier PfisterPhys. Rev. Lett., 101 130501 2008.One-way quantum computing allows any quantum algorithm to be implemented easily using just measurements. The difficult part is creating the universal resource, a cluster state, on which the measurements are made. We propose a radically new approach: a scalable method that uses a single, multimode optical parametric oscillator (OPO). The method is very efficient and generates a continuous-variable cluster state, universal for quantum computation, with quantum information encoded in the quadratures of the optical frequency comb of the OPO.
@article{0804.4468, author = {Menicucci, Nicolas C. and Flammia, Steven T. and Pfister, Olivier}, doi = {10.1103/PhysRevLett.101.130501}, archiveprefix = {arXiv}, eprint = {0804.4468}, journal = {Phys. Rev. Lett.}, title = {One-Way Quantum Computing in the Optical Frequency Comb}, volume = {101}, pages = {130501}, year = {2008} } -
 Entangling the optical frequency comb: simultaneous generation of multiple 2x2 and 2x3 continuous-variable cluster states in a single optical parametric oscillatorHussain Zaidi, Nicolas C. Menicucci, Steven T. Flammia, Russell Bloomer, Matthew Pysher, and Olivier PfisterLaser Physics, 18 659 2008.
Entangling the optical frequency comb: simultaneous generation of multiple 2x2 and 2x3 continuous-variable cluster states in a single optical parametric oscillatorHussain Zaidi, Nicolas C. Menicucci, Steven T. Flammia, Russell Bloomer, Matthew Pysher, and Olivier PfisterLaser Physics, 18 659 2008.We report on our research effort to generate large-scale multipartite optical-mode entanglement using as few physical resources as possible. We have previously shown that cluster- and GHZ-type N-partite continuous-variable entanglement can be obtained in an optical resonator that contains a suitably designed second-order nonlinear optical medium, pumped by at most O(N2) fields. In this paper, we show that the frequency comb of such a resonator can be entangled into an arbitrary number of independent 2x2 and 2x3 continuous-variable cluster states by a single optical parametric oscillator pumped by just a few optical modes.
@article{0710.4980, author = {Zaidi, Hussain and Menicucci, Nicolas C. and Flammia, Steven T. and Bloomer, Russell and Pysher, Matthew and Pfister, Olivier}, doi = {10.1134/S1054660X08050186}, archiveprefix = {arXiv}, eprint = {0710.4980}, journal = {Laser Physics}, title = {Entangling the optical frequency comb: simultaneous generation of multiple 2x2 and 2x3 continuous-variable cluster states in a single optical parametric oscillator}, volume = {18}, pages = {659}, year = {2008} } -
 Quantum-limited metrology with product statesSergio Boixo, Animesh Datta, Steven T. Flammia, Anil Shaji, Emilio Bagan, and Carlton M. CavesPhys. Rev. A, 77 012317 2007.
Quantum-limited metrology with product statesSergio Boixo, Animesh Datta, Steven T. Flammia, Anil Shaji, Emilio Bagan, and Carlton M. CavesPhys. Rev. A, 77 012317 2007.We study the performance of initial product states of n-body systems in generalized quantum metrology protocols that involve estimating an unknown coupling constant in a nonlinear k-body (k ≪ n) Hamiltonian. We obtain the theoretical lower bound on the uncertainty in the estimate of the parameter. For arbitrary initial states, the lower bound scales as 1/nk, and for initial product states, it scales as 1/n(k-1/2. We show that the latter scaling can be achieved using simple, separable measurements. We analyze in detail the case of a quadratic Hamiltonian (k = 2), implementable with Bose-Einstein condensates. We formulate a simple model, based on the evolution of angular-momentum coherent states, which explains the O(n-3/2) scaling for k = 2; the model shows that the entanglement generated by the quadratic Hamiltonian does not play a role in the enhanced sensitivity scaling. We show that phase decoherence does not affect the O(n-3/2) sensitivity scaling for initial product states.
@article{0710.0285, author = {Boixo, Sergio and Datta, Animesh and Flammia, Steven T. and Shaji, Anil and Bagan, Emilio and Caves, Carlton M.}, doi = {10.1103/PhysRevA.77.012317}, archiveprefix = {arXiv}, eprint = {0710.0285}, journal = {Phys. Rev. A}, title = {Quantum-limited metrology with product states}, volume = {77}, pages = {012317}, year = {2007} } -
 Phase transition of computational power in the resource states for one-way quantum computationDaniel E. Browne, Matthew B. Elliott, Steven T. Flammia, Seth T. Merkel, Akimasa Miyake, and Anthony J. ShortNew J. Phys., 10 023010 2008.
Phase transition of computational power in the resource states for one-way quantum computationDaniel E. Browne, Matthew B. Elliott, Steven T. Flammia, Seth T. Merkel, Akimasa Miyake, and Anthony J. ShortNew J. Phys., 10 023010 2008.We study how heralded qubit losses during the preparation of a two-dimensional cluster state, a universal resource state for one-way quantum computation, affect its computational power. Above the percolation threshold we present a polynomial-time algorithm that concentrates a universal cluster state, using resources that scale optimally in the size of the original lattice. On the other hand, below the percolation threshold, we show that single qubit measurements on the faulty lattice can be efficiently simulated classically. We observe a phase transition at the threshold when the amount of entanglement in the faulty lattice directly relevant to the computational power changes exponentially.
@article{0709.1729, author = {Browne, Daniel E. and Elliott, Matthew B. and Flammia, Steven T. and Merkel, Seth T. and Miyake, Akimasa and Short, Anthony J.}, doi = {10.1088/1367-2630/10/2/023010}, archiveprefix = {arXiv}, eprint = {0709.1729}, journal = {New J. Phys.}, title = {Phase transition of computational power in the resource states for one-way quantum computation}, volume = {10}, pages = {023010}, year = {2008} } -
 Ultracompact Generation of Continuous-Variable Cluster StatesNicolas C. Menicucci, Steven T. Flammia, Hussain Zaidi, and Olivier PfisterPhys. Rev. A, 76 010302(R) 2007.
Ultracompact Generation of Continuous-Variable Cluster StatesNicolas C. Menicucci, Steven T. Flammia, Hussain Zaidi, and Olivier PfisterPhys. Rev. A, 76 010302(R) 2007.We propose an experimental scheme that has the potential for large-scale realization of continuous-variable (CV) cluster states for universal quantum computation. We do this by mapping CV cluster-state graphs onto two-mode squeezing graphs, which can be engineered into a single optical parametric oscillator (OPO). The desired CV cluster state is produced directly from a joint squeezing operation on the vacuum using a multi-frequency pump beam. This method has potential for ultracompact experimental implementation. As an illustration, we detail an experimental proposal for creating a four-mode square CV cluster state with a single OPO.
@article{quant-ph/0703096, author = {Menicucci, Nicolas C. and Flammia, Steven T. and Zaidi, Hussain and Pfister, Olivier}, doi = {10.1103/PhysRevA.76.010302}, eprint = {quant-ph/0703096}, journal = {Phys. Rev. A}, title = {Ultracompact Generation of Continuous-Variable Cluster States}, volume = {76}, pages = {010302(R)}, year = {2007} } -
 Constrained bounds on measures of entanglementAnimesh Datta, Steven T. Flammia, Anil Shaji, and Carlton M. CavesPhys. Rev. A, 75 062117 2007.
Constrained bounds on measures of entanglementAnimesh Datta, Steven T. Flammia, Anil Shaji, and Carlton M. CavesPhys. Rev. A, 75 062117 2007.Entanglement measures constructed from two positive, but not completely positive maps on density operators are used as constraints in placing bounds on the entanglement of formation, the tangle, and the concurrence of 4 x N mixed states. The maps are the partial transpose map and the Φ-map introduced by Breuer [H.-P. Breuer, Phys. Rev. Lett. 97, 080501 (2006)]. The norm-based entanglement measures constructed from these two maps, called negativity and Φ-negativity, respectively, lead to two sets of bounds on the entanglement of formation, the tangle, and the concurrence. We compare these bounds and identify the sets of 4 x N density operators for which the bounds from one constraint are better than the bounds from the other. In the process, we present a new derivation of the already known bound on the concurrence based on the negativity. We compute new bounds on the three measures of entanglement using both the constraints simultaneously. We demonstrate how such doubly constrained bounds can be constructed. We discuss extensions of our results to bipartite states of higher dimensions and with more than two constraints.
@article{quant-ph/0612049, author = {Datta, Animesh and Flammia, Steven T. and Shaji, Anil and Caves, Carlton M.}, doi = {10.1103/PhysRevA.75.062117}, eprint = {quant-ph/0612049}, journal = {Phys. Rev. A}, title = {Constrained bounds on measures of entanglement}, volume = {75}, pages = {062117}, year = {2007} } -
 Generalized Limits for Single-Parameter Quantum EstimationSergio Boixo, Steven T. Flammia, Carlton M. Caves, and JM GeremiaPhys. Rev. Lett., 98 090401 2007.
Generalized Limits for Single-Parameter Quantum EstimationSergio Boixo, Steven T. Flammia, Carlton M. Caves, and JM GeremiaPhys. Rev. Lett., 98 090401 2007.We develop generalized bounds for quantum single-parameter estimation problems for which the coupling to the parameter is described by intrinsic multi-system interactions. For a Hamiltonian with k-system parameter-sensitive terms, the quantum limit scales as 1/Nk where N is the number of systems. These quantum limits remain valid when the Hamiltonian is augmented by any parameter independent interaction among the systems and when adaptive measurements via parameter-independent coupling to ancillas are allowed.
@article{quant-ph/0609179, author = {Boixo, Sergio and Flammia, Steven T. and Caves, Carlton M. and Geremia, JM}, doi = {10.1103/PhysRevLett.98.090401}, eprint = {quant-ph/0609179}, journal = {Phys. Rev. Lett.}, title = {Generalized Limits for Single-Parameter Quantum Estimation}, volume = {98}, pages = {090401}, year = {2007} } -
 On SIC-POVMs in Prime DimensionsSteven T. FlammiaJ. Phys. A: Math. Gen., 39 13483–13493 2006.
On SIC-POVMs in Prime DimensionsSteven T. FlammiaJ. Phys. A: Math. Gen., 39 13483–13493 2006.The generalized Pauli group and its normalizer, the Clifford group, have a rich mathematical structure which is relevant to the problem of constructing symmetric informationally complete POVMs (SIC-POVMs). To date, almost every known SIC-POVM fiducial vector is an eigenstate of a "canonical" unitary in the Clifford group. I show that every canonical unitary in prime dimensions p > 3 lies in the same conjugacy class of the Clifford group and give a class representative for all such dimensions. It follows that if even one such SIC-POVM fiducial vector is an eigenvector of such a unitary, then all of them are (for a given such dimension). I also conjecture that in all dimensions d, the number of conjugacy classes is bounded above by 3 and depends only on d mod 9, and I support this claim with computer computations in all dimensions < 48.
@article{quant-ph/0605050, author = {Flammia, Steven T.}, doi = {10.1088/0305-4470/39/43/007}, eprint = {quant-ph/0605050}, journal = {J. Phys. A: Math. Gen.}, title = {On {SIC-POVM}s in Prime Dimensions}, volume = {39}, pages = {13483--13493}, year = {2006} } -
 Entanglement and the Power of One QubitAnimesh Datta, Steven T. Flammia, and Carlton M. CavesPhys. Rev. A, 72 042316 2005.
Entanglement and the Power of One QubitAnimesh Datta, Steven T. Flammia, and Carlton M. CavesPhys. Rev. A, 72 042316 2005.The "Power of One Qubit" refers to a computational model that has access to only one pure bit of quantum information, along with n qubits in the totally mixed state. This model, though not as powerful as a pure-state quantum computer, is capable of performing some computational tasks exponentially faster than any known classical algorithm. One such task is to estimate with fixed accuracy the normalized trace of a unitary operator that can be implemented efficiently in a quantum circuit. We show that circuits of this type generally lead to entangled states, and we investigate the amount of entanglement possible in such circuits, as measured by the multiplicative negativity. We show that the multiplicative negativity is bounded by a constant, independent of n, for all bipartite divisions of the n+1 qubits, and so becomes, when n is large, a vanishingly small fraction of the maximum possible multiplicative negativity for roughly equal divisions. This suggests that the global nature of entanglement is a more important resource for quantum computation than the magnitude of the entanglement.
@article{quant-ph/0505213, author = {Datta, Animesh and Flammia, Steven T. and Caves, Carlton M.}, doi = {10.1103/PhysRevA.72.042316}, eprint = {quant-ph/0505213}, journal = {Phys. Rev. A}, title = {Entanglement and the Power of One Qubit}, volume = {72}, pages = {042316}, year = {2005} } -
 Minimal Informationally Complete Measurements for Pure StatesSteven T. Flammia, Andrew Silberfarb, and Carlton M. CavesFoundations of Physics, 35 1985–2006 2005.
Minimal Informationally Complete Measurements for Pure StatesSteven T. Flammia, Andrew Silberfarb, and Carlton M. CavesFoundations of Physics, 35 1985–2006 2005.We consider measurements, described by a positive-operator-valued measure (POVM), whose outcome probabilities determine an arbitrary pure state of a D-dimensional quantum system. We call such a measurement a pure-state informationally complete (PSI-complete) POVM. We show that a measurement with 2D-1 outcomes cannot be PSI-complete, and then we construct a POVM with 2D outcomes that suffices, thus showing that a minimal PSI-complete POVM has 2D outcomes. We also consider PSI-complete POVMs that have only rank-one POVM elements and construct an example with 3D-2 outcomes, which is a generalization of the tetrahedral measurement for a qubit. The question of the minimal number of elements in a rank-one PSI-complete POVM is left open.
@article{quant-ph/0404137, author = {Flammia, Steven T. and Silberfarb, Andrew and Caves, Carlton M.}, doi = {10.1007/s10701-005-8658-z}, eprint = {quant-ph/0404137}, journal = {Foundations of Physics}, title = {Minimal Informationally Complete Measurements for Pure States}, volume = {35}, pages = {1985--2006}, year = {2005} }